Partie 1 - Mesure de la vitesse initiale d'une balle de golf Le radar placé derrière le joueur utilise un émetteur qui génère une onde électromagnétique de fréquence f
E = 21,125 GHz ainsi qu'un récepteur qui capte l'onde après réflexion sur la balle.
La différence
Df des fréquences émise er reçue permet d'accéder à la vitesse de la balle :
|
Df| = 2 v f
E / c = 4 225 Hz.
Q1 - Nommer le phénomène physique lié à ce décalage.
Effet Doppler.
Q2- Calculer la vitesse initiale v
0 de la balle.
v
0 =
|Df| c / (2 fE)=4225 x3,0 108 / (2 x21,125 109)=30,0 m /s.
Partie 2. Conditions de réalisation d'un slam dunk.
A l'instant initial, le centre de masse G est positionné à une hauteur
h du sol et à une distance d du trou. La balle est lancée dans le plan
verticale avec une vitesse initiale v
0 faisant un angle
a avec l'horizontale.
On néglige les frottements ainsi que la rotation de la balle.
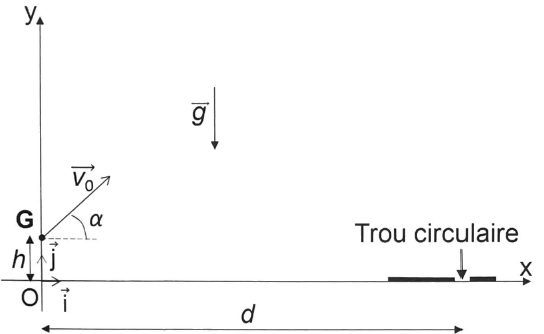
Masse de la balle m = 46 g.
h = 3,0 cm ; d = 150 m.
Q3- Déterminer les expressions littérales des coordonnées du vecteur accélération.
La balle n'est soumise qu'à son poids ; la seconde loi de Newton conduit à :
a
x=0 ; a
y =-g.
Q4. Déterminer les équations horaires du mouvement.
La vitesse est une primitive de l'accélération :
v
x =
V0 cos (a) ; vy = -gt + V0 sin (a).
La position est une primitive de la vitesse :
x(t) = V
0 cos (
a) t ; y = -½gt
2 +
V0 sin (a) t +h.
Q5. En déduire l'équation de la trajectoire.
t = x(t) / (
V0 cos (a)) ;
repport dans y :
y(x) = -½gx
2 / [
V0 cos (a)]
2 +x tan(
a)+h.
Q6. Indiquer les paramètres initiaux de lancement sur lesquels la joueuse peut intervenir pour réussir le slam dunk.
L'angle
a et la vitesse initiale.
Une joueuse frappe la balle avec un angle
a = 39 ° et une vitesse v
0 = 30 m /s.
Q7. Le slam dunk est-il réussi ?
0 =
-0,5 x9,81x2 / [30 cos (39)]2 +x tan(30)+0,03.
0=-9,02 10-3 x2 +0,577 x +0,03.
x2 -63,97 x -3,326 =0.
Discriminant : 63,972 +4 x3,326 =4,10 103 = 64,072.
On retient la racine positive : x =(63,97 +64,07) / 2=64,0 m.
Le slam dunk n'est pas réussi.