Le trombone de Koenig, Bac Centres étrangers 1 2025

Il est composé de deux tubes emboîtés l'un dans l'autre. Le premier est fixe, l'autre est mobile.
Un haut parleur émet un son de fréquence fixe. Un microphone branché sur un oscilloscope mesure le signal à la sortie du dispositif. Les ondes ont la même amplitude dans les deux tubes et leur ppropagation a lieu sans amortissement.
Lorsque le tube mobile est enfoncé au maximum ( décalage nul) le dispositif est symétrique et les deux chemins suivis par les ondes ont la même longueur. Lorsque le tube mobile est tiré, les deux chemins suivis sont différents : les ondes interfèrent.

Q1. Justifier en quoi le trombone de Koenig est un dispositif qui vérifie les onditions nécessaiires à l'observation d'interfèrences au niveau du microphone.
Les deux ondes circulant dans les tubes sont cohérentes, ayant la même fréquence ; le déphasage est constant lorsque le tube mobile est immobilisé.
Sur l'écran de l'oscilloscope on observe la figure suivante :

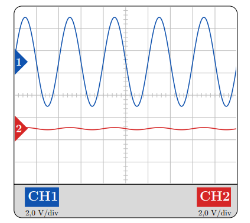
voie 1 reliée au GBF et voie 2 reliée au microphone.
Q2. Préciser le type d'interférences observé et justifier.
Microphone : l'amplitude de l'onde est très faible : les interférences sont destructrices ( expérience 1).
Q3. Exprimer la différence de marche d en fonction de D.
Les ondes passant par le tube mobile parcourent une distance plus longue de 2 D.
d = 2D.
Q4. Rappeler la relation entre d et l, la longueur d'onde du signal sonore dans le cas d'interférences constructives.
d = k l avec k entier relatif.
Q5 - Montrer que la distance de décalage correspondante D_k conduisant à des interférences constructives s'écrit :
D_k = ½k v / f.
v : célérité de l'onde sonore dans le trombone en m/s.
f fréquence de l'onde sonore en Hz.
d = 2 D_k = k l avec l = v / f.
2 D_k = k v / f ; D_k = ½k v / f.
La plus petite distance de décalage permettant d'observver des interférences constructives est D₁ = 4,35 cm pour une fréquence f = 4032 Hz.
Q6. En déduire la célérité de l'onde.
v = 2 D₁ f = 2 x 0,0435 x4032 =351 m /s.