Saut
de puce.
Température au sein d'un igloo. Bac centres étrangers 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Elle
se déplace le plus souvent en sautant et son saut possède des
caractéristiques exceptionnelles puisque qu’il peut atteindre une
hauteur de près de 30 cm.
Lors d’une étude menée avec une caméra ultrarapide, la vitesse du
centre de masse G d’une puce qui saute verticalement a pu être mesurée
dans les instants proches du décollage.
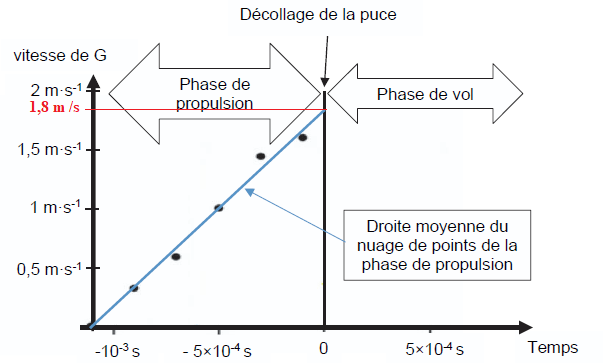
Durant la phase de propulsion, les pattes de la puce sont en contact
avec le support. Le décollage correspond au moment où il n’y a plus
contact. L’étude est menée dans le référentiel terrestre supposé
galiléen. On se place dans le repère (O, x, y)
l'axe vertical étant orienté vers le haut. Dans le cadre du modèle
choisi, les actions mécaniques liées à l’air sont négligées.
Étude de l’accélération en
phase de propulsion.
Q1. En utilisant
la figure, relever la valeur de la vitesse atteinte par la puce à la
fin de la phase de propulsion (t = 0). On admet que l’accélération est
constante durant cette phase.
1,8 m /s.
Q2. Montrer que la
valeur de l’accélération est d’environ 1,5 × 103 m·s-2.
Coefficient directeur de la droite bleue : 1,8 / 10-3 = 1,8 × 103 m·s-2.
Étude du mouvement de la puce en phase de
vol.
La puce, à l’instant t = 0 s, est située à l’origine O du repère
et réalise un saut vertical vers le haut à une vitesse v0 =
1,7 m·s-1.
Q3. À l’aide de la
deuxième loi de Newton, déterminer les coordonnées du vecteur
accélération de
G, centre de masse de la puce durant la phase de vol.
La puce est soumise uniquement à son poids mg.
La seconde loi de Newton conduit à : ax=0 ; ay =
-g.
Q4. Montrer que
les coordonnées du vecteur vitesse de G ont pour expression :
vx(t) = 0 ; vy(t) = - g t + v0.
La vitesse est une primitive de l'accélération et la vitesse initiale
est verticale de norme v0.
vx = 0 ; vy = - g t + v0.
Q5. Déduire de Q4 que les équations
horaires du mouvement de G sont :
x(t) = 0 ; y(t) = - ½gt2+v0t.
La position est une primitive de la vitesse et la position initiale est
l'origine de l'axe.
x(t) = 0 ; y(t) = - ½gt2+v0t.
On admet que la puce
atteint le sommet de son saut à tmax = 0,17 s.
Q6. En déduire la
hauteur ymax atteinte par la puce au sommet de son saut.
Commenter ce résultat au regard de la situation
La composante verticale de la vitesse est nulle au sommet de la
trajectoire.
tmax = v0 / g=1,8 / 9,8 =0,18 s.
ymax = -
4,9 x0,182+1,8x0,18 =0,17 m.
Cette valeur est très inférieure à celle annonée ( 30 cm). Il faudrait
tenir compte de l'action de l'air.
|
...
|
....
|
L’objectif de cet exercice est de comparer l’évolution de la température au sein de l’igloo dans différentes situations.
Données :
- l’igloo est modélisé par une demi-sphère creuse dont l’aire de la surface extérieure
S = 9,0 m2 et d’épaisseur e = 25 cm ;
- l’aire de la surface intérieure de la demi-sphère peut être assimilée à S.
- on suppose que la résistance thermique Rth en K·W-1 de la paroi de l’igloo est liée à son épaisseur e, à l’aire S de la paroi et à la conductivité thermique l en W·m-1·K-1 du matériau par la relation :
Rth=e /(l S).
- la résistance thermique d’une paroi composée de plusieurs couches est la somme des résistances thermiques de chaque couche.
La température extérieure Text = −30 °C est supposée constante. Le système étudié est l’air intérieur.
Le système a une température homogène notée Tint à un instant donné. La personne se trouvant dans l’igloo est assimilée à une source thermique qui dégage un flux thermique F1 de 13 MJ par jour.
On suppose que les résistances thermiques associées aux échanges
thermiques conductoconvectifs de part et d’autre de la paroi de l’igloo
sont négligeables devant Rth.
- on néglige dans cet exercice la fonte de la paroi de l’igloo ainsi que les transferts thermiques avec le sol .
Q1. Citer les trois modes de transferts thermiques.
Conduction, convection, rayonnement.
Q2. Montrer que la valeur du flux thermique F1 produit par la personne est de 1,5 × 102W environ.
13 106 / (24x3600)=1,5 × 102W.
Q3. Déterminer le
sens de variation de la résistance thermique d’une paroi d’épaisseur e
lorsque la conductivité thermique du matériau constituant celle-ci
augmente.
l figure au dénominateur de l'expression de Rth. Si l croît, Rth diminue.
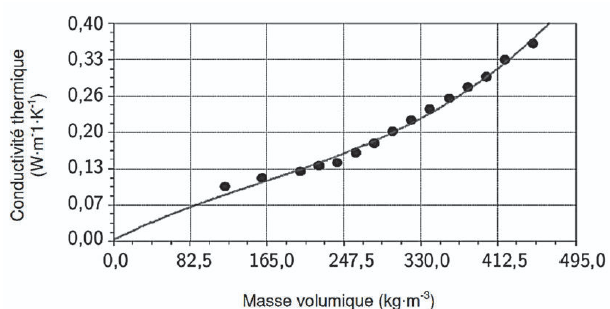
Q4. Discuter, à l’aide de la figure ci-dessus, de l’efficacité de l’isolation thermique de la paroi de l’igloo si
la neige a été très tassée lors de la réalisation de l’igloo. Proposer une explication.
La masse volumique de la neige croît si on la tasse. La conductivité
thermique de la neige augmente et la résistance thermique diminue.
La neige tassée contient moins d'air : l'air est un excellent isolant thermique.
Dans les questions suivantes, on s’intéresse à l’évolution de la température Tint à l’intérieur de l’igloo.
On considère une neige de conductivité thermique l = 0,15 W·m-1·K-1.
Q5. Rappeler la
relation entre le flux thermique traversant une paroi, la différence de
température de part et d’autre de la paroi et la résistance thermique
de la paroi. Déterminer la valeur de F2, le flux thermique sortant à travers la paroi de l’igloo, pour une température intérieure initialement égale à Tint = 0 °C.
F2=(Tint-Text) / Rth.
Rth =e /(l S)= 0,25 /(0,15 x 9)= 0,185 K·W-1.
F2=(-30-0) / 0,185 =-1,6 102 W.
Q6. Déterminer par un raisonnement qualitatif si la température intérieure Tint va diminuer, augmenter ou stagner en comparant les flux F1 et F2.
F2
est négatif, l'intérieur reçoit plus d'air extérieur froid que d'air
chaud dégagé par la personne : la température intérieure va diminuer.
À la suite d’une chute de neige, l’igloo est désormais recouvert de e’
= 3,0 cm de neige fraîche, appelée poudreuse, de conductivité thermique
l’ = 0,040 W·m-1·K-1.
Q7. On suppose que l’aire S n’a pas varié. Montrer que la valeur de la nouvelle résistance thermique de l’igloo est environ Rth’ = 0,27 K·W-1.
Rth’ =Rth +e’ / ( l’ S) =0,185 + 0,030 /(0,040 x9)=0,27 K·W-1.
Q8. Vérifier
qu’alors la valeur de la température à l’intérieur de l’igloo lorsque
l’équilibre thermique est atteint est d’environ 10 °C. Discuter des
hypothèses simplificatrices indiquées dans les données de l’exercice.
L'air intérieur cède à l'extérieur autant de chaleur qu'il n'en reçoit : F1+F2=0.
F1+(Text-Tint) / Rth’=0
Text-Tint= - F1 Rth’.
Tint= Text +F1 Rth’.
Tint= -30 +0,27 x150 ~ 10°C.
On a négligé la fonte de la paroi de l'igloo ainsi que les transferts
thermiques avec le sol. Ces derniers prennent de la chaleur à l'air
intérieur. La température intérieure sera inférieure à 10 °C.
|
|
|
|