Datation
d'une roche. Bac métropole 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Les
phénomènes de radioactivité permettent, en géologie, la datation des
roches. Il est par exemple possible d’utiliser le strontium 87 (87Sr),
qui est notamment issu de la désintégration du rubidium 87 (87Rb),
lui-même également présent dans une roche.
Les objectifs de cet exercice sont d’étudier le principe de la datation
au strontium 87, puis d’utiliser des résultats d’analyse pour
déterminer l’âge d’une roche du site de Meymac situé dans le
département de la Corrèze, site âgé de plusieurs centaines de millions
d’années.
Données :
- temps de demi-vie du noyau de rubidium 87 exprimé en années (a) : t½
= 49,2×109 a ;
- constante radioactive du noyau de rubidium 87 : l = 1,41×10–11 an–1
;
- on suppose qu’une datation d’un échantillon de 1 g de roche par le
rubidium 87 radioactif est possible
tant qu’il reste au moins Nmin = 2,0×109 noyaux
de rubidium 87 dans l’échantillon ;
- extrait du diagramme (N,Z) : les cases grises indiquent les éléments
stables.
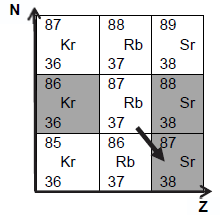
1. Le rubidium 87,
un isotope radioactif adapté pour dater une roche
Q1. Rappeler la
définition de noyaux isotopes.
Deux isotopes ne possèdent pas le même nombre de neutons. Ils ont le
même numéro atomique Z.
Q2. Écrire
l’équation de la désintégration du rubidium 87 indiquée par la flèche
sur l’extrait du
diagramme (N,Z).
8737Rb--> 8738Sr
+0-1e.
Q3. Préciser à quel
type de désintégration correspond cette transformation nucléaire.
Type ß- : émission d'un électron.
On estime qu’un échantillon de 1 g de roche du site de Meymac contenait
à sa formation NRb(0) = 5,8×1020 noyaux de
rubidium 87. On souhaite déterminer l’âge maximal d’une roche qu’il
serait
possible de déterminer par une datation au rubidium 87 d’un échantillon
de 1 g.
Q4. Rappeler la
définition du temps de demi-vie t½.
A t½ la moitié des noyaux initiaux se sont désintégrés.
Q5. Déterminer, en
justifiant le résultat, le nombre maximal de demi-vies après lequel il
reste suffisamment de rubidium 87 dans l’échantillon pour qu’on puisse
le détecter.
On remarquera que le rapport 5,8×1020 / (2,0×109
) est compris entre 238 et 239.
N(t) doit être supérieur à N0 / 2n ; N0
/ Nmin = 2n.
n = 38.
Q6. Justifier que
le rubidium 87 est adapté pour dater un échantillon de 1 g de roche du
site de Meymac.
On peut dater le rubidium 87 jusqu'à 38 t½ soit 1,9 1012
ans ; ce qui est bien supérieur à l'âge du site.
|
...
|
....
|
2. Décroissance radioactive du
rubidium 87 dans une roche
La désintégration spontanée des noyaux de rubidium 87 présents dans un
échantillon de 1 g de roche suit la
loi de décroissance radioactive. Le nombre NRb(t) de noyaux
de rubidium 87 présents dans un échantillon de
roche à la date t est solution de l’équation différentielle suivante :
dNRb(t)/dt= – l∙NRb(t)
Q7. Vérifier que NRb(t)
= NRb(0)·e– l·t
est solution de l’équation différentielle ci-dessus.
dNRb(t)/dt=-NRb(0) l e– l·t ;
repport dans l'équation : -NRb(0) l e– l·t = – l∙NRb(t) est
vérifié quelque soit le temps.
On appelle tf la date à laquelle il reste Nmin =
2,0×109 noyaux de rubidium 87 dans l’échantillon.
Q8. Déterminer
l’expression de tf en fonction de Nmin, NRb(0)
et l.
Nmin = NRb(0)·exp(– l·t f) ; Nmin
/ NRb(0) =exp(– l·t
f) ;
ln(Nmin / NRb(0) =– l·t f ;
t f = ln(NRb(0) /Nmin) / l.
Q9. Calculer la
valeur de tf puis la comparer à la réponse donnée dans la
question Q6. Commenter.
tf = ln(5,8 1020/ (2,0 109)) /(1,41 10-11)=1,9
1012 ans.
On retrouve la valeur donnée en Q6.
3. Datation d’une
roche du site de Meymac au strontium 87
On considère que la quantité de strontium 87 formé au cours du temps
dans la roche est uniquement issue
de la désintégration du rubidium 87. La quantité de strontium 87
présent dans la roche à une date t s’écrit :
NSr(t) = NSr(0) + NSr formé(t)
Équation 1
avec :
- NSr(t) : nombre de noyaux de strontium 87 présents à la
date t ;
- NSr(0) : nombre de noyaux de strontium 87 présents à la
date t = 0 ;
- NSr formé(t) : nombre de noyaux de strontium 87 formés par
la désintégration du rubidium 87 à la date t.
Q10. Donner la
relation entre NSr formé(t), NRb(0)
et NRb(t), sachant que pour un noyau de rubidium 87 qui se
désintègre, un noyau de strontium 87 se forme.
NSr formé(t)= NRb(0) - NRb(t).
Q11. En déduire
l’égalité :
NSr formé(t) = NRb(t)·( exp(lt) – 1) Équation 2
NRb(t) = NRb(0)·e– l·t ;
NSr formé(t) =NRb(0)-NRb(t) ; NRb(0)=NRb(t)·/
e– l·t
.
NSr formé(t) =NRb(t)·/ e– l·t -NRb(t)
=NRb(t) (1 / e– l·t
-1)=NRb(t) ( el·t
-1)
Les équations 1 et 2 permettent enfin d’obtenir l’équation 3 :
NSr(t) / Nréf= NSr(0) / Nréf+
( el·t
-1) · NRb(t) / Nréf Équation 3
où Nréf représente le nombre de noyaux stables de strontium
86, supposé constant au cours du temps.
On écrit l’équation 3 sous la forme y = b + ( el·t -1)·x avec y
= NSr(t) / Nréf, b = NSr(0) / Nréf
et x =NRb(t) / Nréf
, dans laquelle :
- y et x sont des grandeurs mesurables par les géologues pour un
ensemble d’échantillons prélevés dans une roche donnée ;
- b est une grandeur indépendante de l’échantillon.
Plusieurs échantillons de roche du site de Meymac sont prélevés à la
date troche correspondant à l’âge de la
roche. Pour chaque échantillon, on mesure les grandeurs x et y. Les
résultats obtenus sont présentés sur la
figure 1 ci-après :
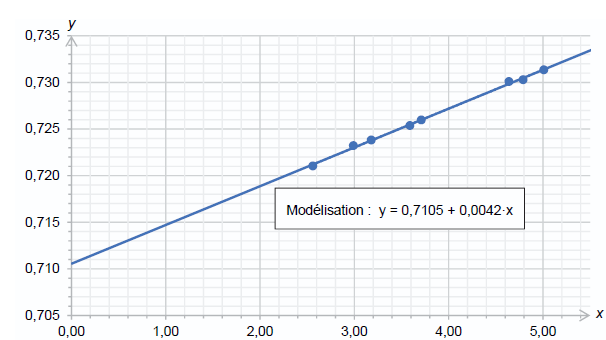
Q12. Déterminer
l’âge troche de la roche du site de Meymac.
el·t
-1 =0,0042 ; el·t
=1,0042 ; lt
=ln(1,0042)=4,19 10-3 ;
t = 4,19 10-3/(1,41 10-11)=2,97 108
ans |
|
|
|