Viscosimètre à chute libre. Bac métropole 2025.

Certains équipements mécaniques, comme les moteurs, nécessitent l’utilisation d’huiles de valeur de viscosité contrôlée pour pouvoir fonctionner correctement.
Le but de cet exercice est d’étudier le principe de fonctionnement d’un viscosimètre à chute de bille permettant de mesurer, à température ambiante, la viscosité d’une huile appelée « huile C ».
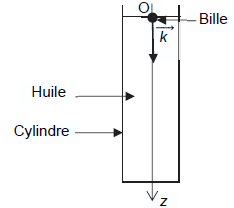
La mesure de la viscosité de l’huile C repose sur l’exploitation de la chute verticale d’une bille en acier dans un récipient cylindrique, rempli de cette huile. Le mouvement du centre de masse de la bille est étudié dans le référentiel terrestre supposé galiléen, muni d’un repère d’origine O, d’axe vertical (Oz) orienté vers le bas et de vecteur unitaire k . La situation est schématisée sur la figure 1.

- masse volumique de l’huile C : rh = 8,31×10² kg·m^–3 ;
- masse volumique de la bille : rb= 1,06×10³ kg·m^–3 ;
- rayon de la bille r = 0,993 mm ;
- intensité de la pesanteur terrestre : g = 9,81 m·s^–2 ;
- pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le
quotient | x - x_ref| /u(x) avec x la valeur mesurée, x_ref la valeur de référence et u(x) l’incertitude-type associée
à la valeur mesurée x.
Lors de sa chute verticale dans l’huile C, la bille de masse m est soumise à trois forces :
- son poids noté P ;
- la poussée d’Archimède, exercée par l’huile, d’expression vectorielle P_A = rh∙V_b·g∙;
- la force de frottement exercée par l’huile sur la bille: f = a∙n_C∙v avec a une constante homogène à une distance, dépendant des paramètres géométriques du système, n_C la viscosité de l’huile C et v la valeur de la vitesse du centre
de masse de la bille. On donne a = 1,92×10^–2 m.
Q1. Montrer, à l’aide d’un raisonnement sur les unités, que la viscosité n_C s’exprime en N·m^–2·s.
n_C : force / (distance x vitesse) soit N m^-2 s.
À la date t = 0, la bille est lâchée avec une vitesse initiale nulle depuis le point O, situé dans l’huile, en haut du récipient cylindrique. Au bout de quelques instants, le mouvement de la bille devient rectiligne uniforme, la bille atteint alors une vitesse limite notée v_lim.
Q2. Préciser, en justifiant, si la valeur de la force de frottement augmente ou diminue quand la valeur de la vitesse de la bille augmente.
La force de frottement étant proportionnelle à la vitesse, f augmente si la vitesse augmente.
Q3. Représenter sur un schéma, sans calcul et en justifiant, l’ensemble des forces appliquées au système {bille}, lorsque la vitesse limite est atteinte.
La somme vectorielle des forces est nulle quand la vitese limite est atteinte.

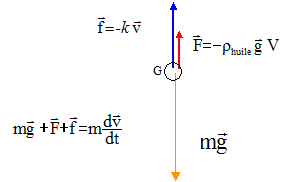Q4. Montrer que la vitesse limite vérifie l’équation :
mg = a∙n_C∙v_lim +rh∙V_b·g∙avec m = V_b· rb
a∙n_C∙v_lim =V_b·g ( rb -rh)
V_b = 4 /3 pr³ ; a∙n_C∙v_lim =4 /3 pr³·g ( rb -rh).
Q5. La valeur limite de la vitesse de la bille vaut v_lim= 5,37 mm·s^–1. Calculer la valeur de la viscosité ∙n_C de
l’huile C.
n_C∙= 4 /3 pr³·g ( rb -rh)/( a v_lim)=4 /3 x3,14 x(9,93 10^-4)³ x9,81 (1,06 10³-8,31 10²) /(5,37 10^-3x1,92 10^-2)=8,94 10^-2 = 0,089 N·m^–2·s.
L’huile C a une viscosité de référence qui vaut n_réf = 0,093 N·m^–2·s et l’incertitude-type sur la valeur de la
viscosité ηC obtenue vaut u(ηC) = 0,003 N·m^–2·s.
Q6. Déterminer si la valeur de la viscosité ηC obtenue expérimentalement est en accord avec la valeur de référence.
(0,093-0,089) / 0,003 =1,3 < 2.
Donc accord avec la valeur de référence.