....
|
L’objectif
de l’exercice est de modéliser le mouvement de la planète Kepler-1658b
tout d’abord au cours d’une révolution, puis sur une échelle de temps
plus longue.
Données :
− masse de la planète Kepler-1658b : m = 1,12×1028 kg ;
− période de révolution de la planète Kepler-1658b autour de son étoile en 2023 :
T = 3,85 jours ;
− masse de l’étoile Kepler-1658 : M = 2,88×1030 kg ;
− constante universelle de la gravitation : G = 6,67×10-11 N·kg-2·m2 ;
La planète Kepler-1658b est assimilée à son centre de masse, P, dans le
référentiel centré sur l’étoile Kepler-1658 et dont les axes pointent
vers trois étoiles lointaines de directions à peu près constantes. On
suppose ce référentiel galiléen au regard des durées et des distances
mises en jeu.
Dans un premier temps, on modélise la trajectoire de P par un cercle
dont le rayon est noté r et dont le centre correspond au centre de
masse de l’étoile, noté E.
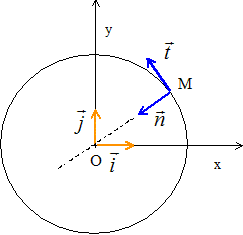
Q1. Dans
l’hypothèse d’un mouvement circulaire, schématiser la trajectoire de P
autour de E sans souci d’échelle. Représenter le repère de Frenet
associé à la planète en indiquant les vecteurs unitaires
constituant la base de ce repère.
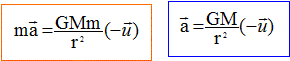
Q2. Déterminer, à l’aide de la deuxième loi de Newton, l’expression vectorielle de l’accélération de
P, en fonction de G, m, r et de la base de Frenet.
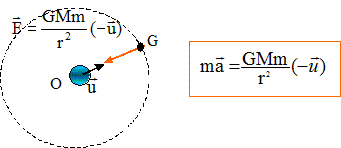
Q3. Dans cette
hypothèse du mouvement circulaire, en déduire que le mouvement de P est
uniforme et montrer que l’expression de la norme de son vecteur vitesse
est : v2 = GM / r.
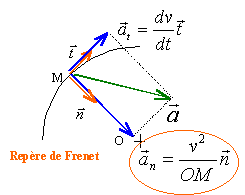
L'accélération normale vaut v2 / r et l'accélération tangentielle dv / dt est nulle.
Par conséquent la norme du vecteur vitesse est constante et le mouvement est uniforme.
Accélération normale = v2 /r =GM / r2 ; v2 = GM/ r.
On note T la période de révolution de P autour de E.
Q4. Montrer que l’expression du rayon de l’orbite de la planète représentée par le point P vérifie la relation :
r3 =GMT2 /(4p2).
La planète décrit la circonférence 2 pr à la vitesse v en T seconde.
2pr = vT ; 4p2r2 = v2T2 =GM / r T2.
r3 =GMT2 /(4p2).
Q5. Déterminer la valeur de r et la comparer avec les données de l’article 7,25 millions de km.
r3 = 6,67 10-11 x2,88 1030x(3,85 x24 x3600)2 / (4 x3,142)=5,38 1029.
r =8,13 109 m = 8,13 106 km.
Cette valeur est du même ordre de gtandeur que la valeur donnée dans l'article.
Dans leur article paru en décembre 2022, une équipe
d’astronomes a montré que la valeur de la période de révolution de la
planète Kepler-1658b diminuait de 131 ms par année terrestre.
Q6. En admettant
que cette diminution est invariante au cours du temps, vérifier qu’à
chaque révolution, la période de révolution de la planète Kepler-1658b
diminue de DT = 1,38 ms.
T = 3,85 jours ; 365 / 3,85 =94,8.
DT =131 / 94,8=1,38 ms.
Q7. Comparer cette
diminution avec la période de révolution et justifier que la période T
peut être considérée constante pour un faible nombre de révolutions.
DT / T = 1,38 10-3 / (3,85 x24x3600)~4 10-9.
DT est négligeable devant T pour un petit nombre de révolutions.
Q8. Déterminer
qualitativement, à l’aide de l’expression donnée à la question Q4 qu’on
supposera encore valide, si le rayon de l’orbite augmente ou diminue
légèrement à chaque révolution.
r3 =GMT2 /(4p2).
Si T diminue alors r diminue.
Pour un grand nombre de révolutions, le mouvement de la planète
Kepler-1658b est modélisé par une succession de trajectoires quasi
circulaires dont le rayon varie à chaque révolution.
La période passe de 3,85 jours à 1600 s :
diminution de la période =3,85 x24x3600 -1600 =3,31 105s
Q9. Le calcul de
la période de révolution de la planète juste avant l’impact prévoit une
valeur beaucoup plus faible (1 600 s) que celle de 2023 indiquée dans
les données. En considérant que la période diminue de 131 ms par année
terrestre, confirmer la prévision « si elle se
rapproche toujours au même rythme, elle entrera en collision avec celle-ci dans près de trois millions d'années ».
Diminution de la période au cours de x années : 3,85 x3600x24-1600 =3,31 105 ms.
x = 3,31 105 / 0,131 ~2,5 106 années, de l'ordre de 3 millions d'années.
|