Ariane
6 : un déluge d'eau pour se protéger du bruit. Position
de l'ISS en temps réel.
Bac métropole 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Le
9 juillet 2024, la fusée Ariane 6 a décollé avec succès depuis le
Centre spatial guyanais de
Kourou.
Au moment du décollage, 800 000 litres d’eau sont déversés sur le pas
de tir (au pied de la fusée)
en quelques dizaines de secondes, c’est ce que l’on appelle le déluge.
En plus de l’atténuation des effets thermiques du décollage, l’objectif
principal du déluge est de faire comme un mur d’eau qui absorbe en
partie l’onde acoustique produite par le décollage et atténue le niveau
sonore qui aurait pu atteindre, sinon, 180 dB.
Un observateur se place dans un premier temps à une distance d1
= 1,0 m du pas de tir. Sans déluge d’eau, le niveau d’intensité sonore
perçu à la distance d1 = 1,0 m vaut L1,sans = 180
dB.
Avec le déluge, l’intensité sonore vaut I1,avec = 0,10
W.m-2.
Q1. Montrer que le
niveau d’intensité sonore L1,avec du son produit au
décollage à la distance d1 = 1,0 m après son passage à travers le mur
d’eau vaut L1,avec = 110 dB.
L1,avec = 10 log (I1,avec / I0)=20
log(0,10 / 10-12)=10 x11 =110 dB.
Q2. Indiquer si cet observateur
encourt un risque auditif au moment du décollage en présence du déluge
d’eau.
La durée maximale d'exposition à un tel bruit est de 1 minute par jour.
l'observateur présente un risque auditif.
Q3. Calculer
l’atténuation Aavec = L1,sans - L1,avec
en décibels qui a alors lieu grâce au déluge d’eau.
Aavec =180-110=70 dB.
L’observateur se trouve
désormais à une distance d2 du pas de tir.
Q4. En l’absence
du déluge d’eau, estimer la valeur de la distance d2 de
sorte que le niveau sonore ne dépasse pas L2,sans = 95 dB.
Atténuation lorsqu'on passe d'une distance d1 à une
distance d2 de la source sonore :
L1,avec -L2,sans =20 log(d2/d1) ; 180-95=
20 log(d2 / 1) ;
log(d2) = 85 / 20 =4,25 ; d2 =1,8 104
m = 18 km..
Les fusées Ariane sont lancées depuis Kourou, en Guyane française. Le
site d’observation est situé à Carapa à 18 km du pas de tir.
Q5. Commenter
l’intérêt acoustique du déluge d’eau pour un observateur situé à Carapa.
Pour cet observateur, sans déluge d'eau,
le niveau sonore serait de 95 dB : la durée maximale d'exposition est
de 15 minutes par jour. Le décollage dure moins de 15 min : le mur
d'eau n'a pas d'intérêt si on se trouve loin du pas de tir.
Avec un mur d'eau, le niveau sonore dû au décollage reçu à Carapa
est de 25 dB, à peine perceptible.
|
...
|
....
|
La
station spatiale internationale (ISS) est en orbite quasi circulaire
autour de la Terre. Elle abrite un équipage d’astronautes qui se
consacrent à la recherche scientifique dans un environnement spatial.
L’objectif de cet exercice est de vérifier le nombre total (arrondi à
l’entier le plus proche) de levers et de couchers de Soleil auquel les
astronautes assistent chaque jour à partir des données fournies par le
site Astropleiades.
− rayon de la Terre : R = 6,37 × 106 m ;
− constante de gravitation universelle : G = 6,67 × 10–11 m3·kg–1·s–2 ;
− masse de la Terre : M= 5,97 × 1024 kg.
On choisit de modéliser le mouvement du satellite par le mouvement
circulaire uniforme de son centre de masse S sous l’action de la seule
force d’attraction gravitationnelle exercée par la Terre dans le
référentiel géocentrique supposé galiléen au regard des distances et
des durées mises en
jeu.
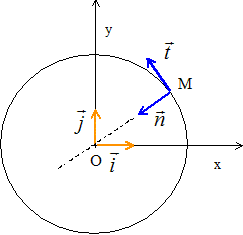
Q1. Réaliser un
schéma simple, sans souci des proportions mises en jeu, de la situation
et y faire figurer la force d’attraction gravitationnelle exercée par
la Terre sur le point S, le rayon R de la Terre, l’altitude h à
laquelle évolue la station ISS et les vecteurs unitaires base de Frenet
placée en S.
Q2. En appliquant la deuxième loi de Newton, établir l’expression du vecteur accélération de S.
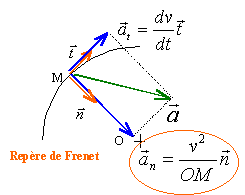
Q3. Représenter, sans souci des proportions, le vecteur accélération.
On note r = R+h.
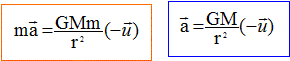
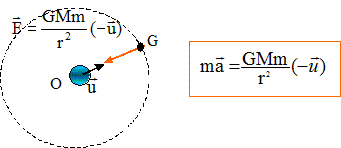
Q4. Montrer que l’expression de la valeur v de la vitesse de l’ISS évoluant autour de la Terre à l’altitude h s’écrit :
v 2= ( G M / r).
L'accélération
normale vaut v2 / r et l'accélération tangentielle dv / dt
est nulle.
Par conséquent la norme du vecteur vitesse est constante et le
mouvement est uniforme.
Accélération normale = v2 /r =GM / r2 ; v2
= GM/ r.
Q5. Déduire, en exploitant la relation précédente, l’expression de la masse M de la Terre en fonction de v, r et G.
M = r v2 / G.
Q6. Relever les
valeurs d’altitude et de vitesse sur la capture d’écran réalisée à
15h15 puis effectuer le calcul de la masse de la Terre M en supposant
que la vitesse et l’altitude sont à peu près constantes.
Altitude 426 km ; vitesse : 27 560 km /h = 27 560 / 3,6 =7,66 103 m /s.
r = 426 + 6,37 103 =6,796 103 km = 6,796 106 m.
M =6,796 106 x(7,66 103)2 /(6,67 10-11)=5,97 1024 kg.
Q7. Calculer la durée T d’une révolution de l’ISS.
La vitesse étant constante v = 2pr / T.
T = 2pr / v = 2 x3,14 x6,796 106 / (7,66 103) =5,57 103 s ou 92,9 min ou 1,548 heure ou 1 h 33 min.
Q8. Les
astronautes, à bord de l’ISS, assistent à environ 16 levers et couchers
de Soleil par jour. Vérifier cette affirmation par un calcul simple.
A chaque révolution, les astronautes assistent à un lever et un coucher de soleil en 1, 55 h.
Nombre de lever et coucher de soleil : 24 / 1,55 ~15,5 soit 16 levers et couchers de soleil. |
|
|
|