Autour
de la glace.
Bac Polynésie 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Datation au plomb 210 d'une carotte de glace en Artique.
Dans l'atmosphère le plomb 210 est issu de la désintégration du radon 222.
Q1. Déterminer le type de désintégration que subit le plomb 210.
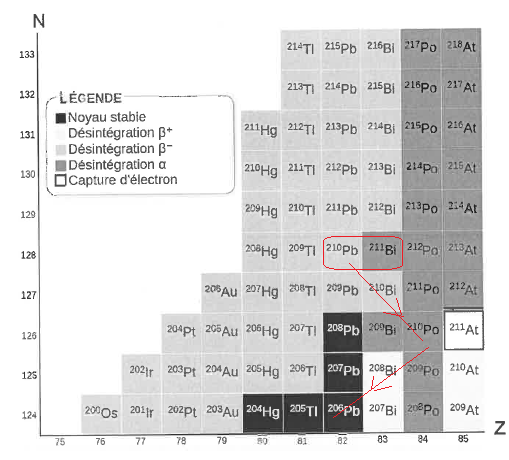
Désintégration ß-.
Q2. Etablir l'équation modélisant la désintégration radioactive du plomb 210 conduisant au bismuth 210.
21082 Pb--> 21083 Bi +0-1 e.
Conservation du nombre de nucléons : 210 = 210 +0.
Conservation de la charge : 82 = 83-1.
Le bismuth 210 subit une désintégration ß- conduisant au polonium 210 instable, il se désintègre à son tour..
Q3. Indiquer le noyau formé.
21083 Bi -->21084 Po + 0-1 e.
21084 Po se désintègre ensuite par émission alpha en 206Pb stable .
21084 Po -->20682 Pb + 4 2He.
Q4. Donner la relation entre l'activité A(t) et la dérivée temporelle du nombre de noyaux radioactifs N(t).
A(t) = -dN(t) /dt.
Q5. Ecrire l'équation différentielle régissant la population de noyaux radioactifs N(t).
A(t) = l N(t) avec l la constante radioactive.
-dN(t) /dt. = l N(t).
dN(t) /dt. + l N(t)=0.
Q6. Vérifier que N(t)=N0 exp(-lt) est solution de cette équation.
On dérive : dN(t)dt = -N0 l exp(-lt).
Repport dans l'équation différentielle : -N0 l exp(-lt)+l N0 l exp(-lt) =0 est vérifiée quel que soit le temps.
Q7. Démontrer que le temps de demi-vie t½ est relié à l par t½ = ln(2) / l. Calculer l du plomb 210.
N(t½)=½N0 = N0exp(-lt½) ; 0,5 =exp(-lt½).
ln(0,5) = -ln(2) = (-lt½).
t½ = ln(2) / l.
t½ (plomb 210) = 22,2 ans ;
l = ln(2) / 22,2 =0,0312 an-1.
A une profondeur de 30 m, une masse de 1 kg de glace a une activité A30 = 4,72 mBq liée au plomb 210. ( mesure faite en 1993). On suppose qu'à sa formation l'activité de 1 kg de glace valait A0 = 110 mBq.
Q8. En déduire
l'année à laquelle la glace présente à 30 m de profondeur s'est formée.
En déduire l'épaisseur moyenne de glace accumulée chaque année.
A(t)= A0 exp (-lt).
4,72 =110 exp(-0,0312 t) ;
0,0429 = exp(-0,0312 t) ;
t =- ln(0,0429) / 0,0312~ 101 ans.
1993-101=1892.
Epaisseur moyenne de glace formée chaque année : 30 / 101 ~0,30 m.
|
...
|
....
|
Contrôle de la grêle par ensemencement à l'iodure d'argent.
Ag+aq + ligand aq = Ag(ligand)+aq.
Q9 et 10. Nommer le type de représentation ainsi que les deux familles fonctionnelle correspondant aux groupes A et B.
Formule topologique.
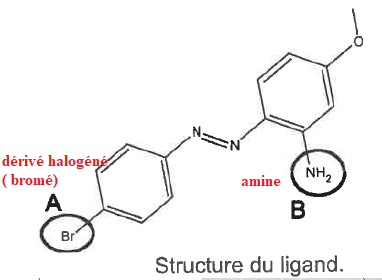
Q11. Ecrire la constante d'équilibre de la réaction de formation de Ag(ligand)+.
K = [Ag(ligand)+] c° /([Ag+] [ligand]).
Q12. Justifier que la réaction est quasi-totale si le ligand est en large excès.
Si le ligand est en large excès, l'équilibre est déplacé vers la droite, formation du complexe Ag+] [ligand].
Les solutions aqueuses contenant Ag+] [ligand] sont colorées. Le maximum d'absorption se situe vers 516 nm.
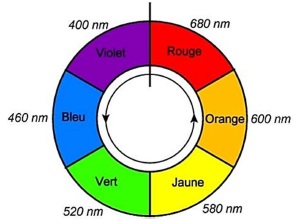
Q13 Déterminer la couleur des solutions acqueuses contenant l'espèce Ag(ligand)+.
513 nm appartient au vert. Les solutions contenant Ag(ligand)+ possèdent la couleur complémentaire du vert soit le rouge.
On mélange VAg+ = 1,0 mL d'une solution ce concentration en ion argent [Ag+] = 7,4 10-6 mol / L avec un volume VL de solution de ligand à la concentration CL = 1,0 10-3 mol / L.
Q14. Calculer la quanttité de matière initiale en ion argent.
nAg = VAg+ [Ag+]=7,4 10-6 x1 = 7,4 10-6 mmol.
On mesure l'absorbance des différentes solutions obtenus à l = 516 nm.
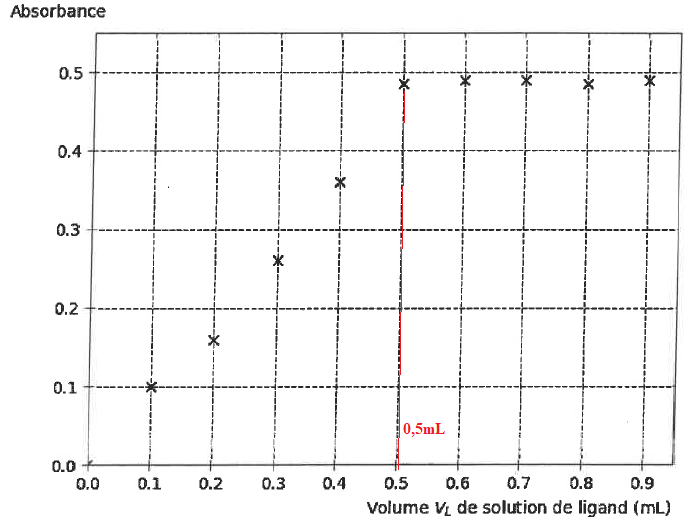
Q15. Déterminer le volume Vtot L de solution de ligand versé pour que l'ensemble des ions Ag+aq présents aient réagi en quasi-totalité. Calculer la quantité de matière nL de ligand introduit.
nL = 0,5 x1,0 10-3 = 5,0 10-4 mol = 0,50 mmol.
Q16. Vérifier que le ligand est en large excès.
nAg= 7,4 10-6 mmol ; nL = 0,5 mmol valeur très supérieure à nAg. La réaction sera totale.
Q17. Montrer que l'absorbance de la solution de l'espèce Ag(ligand)+ est proportionnelle à la concentration en ion argent initialement en solution CAg i.
|
avancement mmol
|
Ag+aq
|
+ligand
|
=Agligand+aq
|
initial
|
0
|
7,4 10-6 |
0,5
|
0
|
en cours
|
x
|
7,4 10-6-x
|
0,5-x
|
x
|
fin ( à l'équilibre)
|
xf
|
7,4 10-6 |
0,5-xf ~0,5
|
xf=7,4 10-6 |
Loi de Beer-Lambert : A = e [Agligand+] l.
A = 6,5 104 c pour des concentrations en masse en ion argent c comprises entre 9,10-3 et 1,5 µg / mL ( 1,5 mg / L).
Q18. Vérifier que
la valeur maximale de la concentration en masse en ion argent est
cohérente avec une limite expérimentale de la loi de Beer-Lambert ( Amax = 0,9 à 516 nm).
1,5 10-3 / M(Ag) =1,5 10-3 / 108 =1,39 10-5 mol / L.
A = 6,5 104 x1,39 10-5=0,9.
|
|
|
|