Le Mölkky. Bac Polynésie 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . . . .. .. ...... ... Le joueur fait tomber des quilles à l'aide d'un bâton afin d'atteindre un score de 50 points. Une quille tombée donne le nombre de points portée sur cette dernière compris entre 1 et 12. Objectif : établir l'équation horaire de la trajectoire du baton lancé ; déterminer le lieu d'impact. On s'intéresse au mouvement du centre de masse  G du bâton qu'un joueur lance afin de faire tomber une quille. 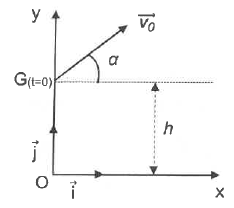Q1. Enoncer la seconde loi de Newton et déterminer les coordonnées du vecteur accélération. La somme vectorielle des forces appliquées à un système est égale au produit de son accélération par la masse du système. Le baton n'est soumis qu'à son poids. ax = 0 ; ay = -g. Q2. Etablir les coordonnées du vecteur vitesse. le vecteur vitesse est une primitive du vecteur accélération et le vecteur vitesse initiale a pour coordonnées v0 cos a ; v0 sin a. vx = v0 cos a ; vy = -gt+ v0 sin a. Q3. Etablir les équations horaires du mouvement. La position est une primitive de la vitesse et la poisition initiale  a pour coordonnées( 0 ; h). x = v0 cos a t ; y = -½gt2 +v0 sin a t +h. Q4. Montrer que l'expression de la trajectoire s'écrit : y = -0,27 x2+0,58 x+0,70. t = x / ( v0 cos a) ; repport dans y : y = -½gx2 / ( v0 cos a)2 +x tan a  +h. v0 = 4,9 m /s ; h = 0,70 m ; a = 30°. y = -4,9 /(4,9 cos 30)2 x2 + x tan 30 +0,70. y = -0,27 x2+0,58 x+0,70. Un joueur ayant déja marqué 41 points s'apprète à lancer le bâton. Pour gagner il doit marquer exactement 50 points. On donne la configuration du jeu avant le lancer. Atribuer chaque courbe à l'énergie représentée en justifiant. La taille des quilles est négligeable et le baton ne rebondit pas. Q5. Vérifier que la partie est gagnée si le lancer est réalisé dans les conditions précédentes. Il faut atteindre la quille n°9 située à 3,0 m du joueur. y(3) =  -0,27 *32+0,58 *3+0,70 = 0,01 ou 1 cm. Le bâton étant à 1 cm du sol va bien renverser la quille n°9. ... .... Le programme Python permet de calculer puis de tracer les courbes représentant les énergies potentielle, cinétique et mécanique du baton lors de son lancer. Q6 . Déterminer la masse du bâton. La ligne 18 donne l'énergie cinétique du bâton : ½mv2 = 0,5 x0,4 (vx2+vy2). m = 0,4 kg. Q7. Compléter la ligne 22. Cette ligne calcule l'énergie mécanique : Em=Ep+Ec Q8. Atribuer chaque courbe à l'énergie représentée en justifiant. 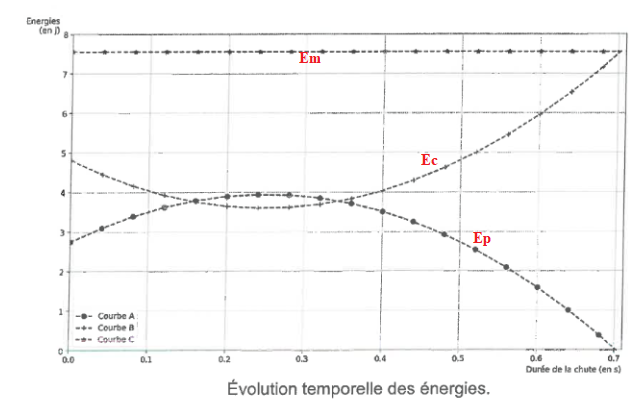Ep = mgy avec y qui augmente puis diminue. Em =Ec+Ep= constante. Au début du lancer, le baton monte et perd de la vitesse ; Ec diminue puis augmente. Q9 Déterminer la durée de vol du bâton et en déduire que la partie décrite précédemment est remportée par le joueur. La durée de vol est égale à 0,7 s. x = v0 cos a t =4,9 x cos 30 x0,7 =3,0 m. Au bout de 0,7 s, le bâton parcourt 3 m et atteint la quille n°9.

menu