Performances
des bolomètres de Planck.
Bac Polynésie 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
L'objectif est d'étudier les performances d'un des bolomètres du satellite Planck.
Le CMB se caractérise par un rayonnement thermique de température caractéristique TCMB
= 2,725 K. Afin d'étudier les variations de température autour de cette
valeur, le satellite Planck est équipé d'un bolomètre sensible au
rayonnement de fréquence f0 = 217 GHz.
Q1. Calculer la longueur d'onde correspondante et nommer le domaine du spectre auquelle elle appartient.
l0 =c / f0 =3,0 108 / (217 109)=1,4 10-3 m= 1,4 mm ( micro-ondes).
Q2. Montrer que la puissance PCMB reçue par le bolomètre de la part du CMB au travers le filtre vaut 7,82 10-14 W.
La puissance reçue par une surface S d'un corps à la température T est 5,67 10-8 T4S.
Surface de la partie sensible du CMB ; S =9,93 10-8 m2. Le filtre placé devant cette surface sélectionne 25,2 % de cette puissance.
PCMB = 5,67 10-8 *2,7254 *9,93 10-8 *0,252=7,82 10-14 W.
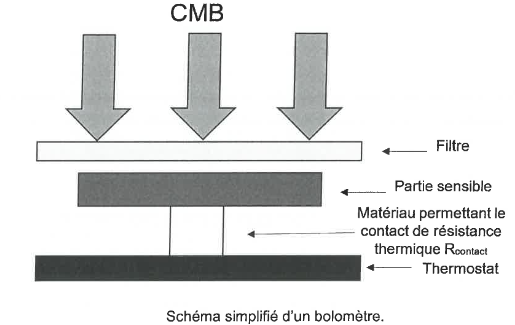
La puissance Psyst reçue par un système à la température Tsyst en contact avec un thermostat à la température T0 par l'intermédiaire d'une résistance thermique Rth s'exprime par :
Psyst = -(Tsyst-T0) / Rth.
Q3. Exprimer la puissance PT reçue par la partie sensible du bolomètre de la part du thermostat en fonction de T, TT et Rcontact. Justifier son signe.
PT = -(T-TT) / Rcontact.
La puissance reçue est positive : T < TT.
Q4. Exprimer le transfert thermique Qtot échangée par la partie sensible du bolomètre avec l'ensemble des sources extérieures pendant une durée Dt en fonction de PCMB, T, TT, Dt et Rcontact.
Qtot =(PCMB+PT) Dt =(PCMB -(T-TT) / Rcontact )Dt.
Q5. Enoncer le premier principe de la thermodynamique en précisant le nom de chaque grandeur et son unité.
.Le premier principe traduit la conservation de l'énergie totale d'un système.
Soit
un système fermé évoluant entre deux état 1 et 2 en recevant de
l'extérieur une quantité de chaleur Q et un travail W (grandeurs
algébriques), la variation de son énergie interne est :
DU = W+Q.
DU variation de l'énergie interne ( J) ; Q quantité de chaleur ( J) ; W : travail ( J).
On démontre que l'équation différentielle régissant l'évolution de la température en fonction du temps est :
dT / dt + T /(Rcontact .Cbolo) =PCMB/Cbolo+TT/(Rcontact Cbolo).
TT = 0,1 K ; Rcontact = 3,75 109 K W-1. Cbolo=0,40 10-12 JK-1.
Q6. Montrer que t = Rcontact Cbolo est homogène à un temps.
Rcontact Cbolo s'exprime en K W-1JK-1soit W-1J.
Or W = J s-1 ; W-1= J-1 s ; W-1J = s.
Q7. Sachant que T (t) = TT+T1(1-exp(-t / t) est solution de l'équation différentielle satisfaisant T(0) = TT, donner l'expression de T1 ainsi que sa valeur.
Au bout d'un temps très long Too = TT+T1.
T1=Too - TT avec Too = TCMB.
T1=TCMB - TT =2,725-0,1 = 2,625 K.
Le bolomètre réalise une mesure de puissance fiable dès que sa température se stabilise au bout de'une durée égale à 5 t.
Afin d'étudier le CMB, le ciel est divisé en petites zones. le satellite Planck balaie chaque zone en Dtscan = 14 ms.
Q8. Montrer que le bolomètre peut obtenir une mesure fiable du CMB.
5 t = 5 x1,5 10-3 =7,5 10-3 s = 7,5 ms.
Dtscan > 5 t ; le bolomètre peut obtenir une mesure fiable du CMB.
|