Mathématiques. QCM. Bac Polynésie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
1. On considère l’équation différentielle : (E) y ′ = ½ y +4.
Affirmation 1 : Les solutions de (E) sont les fonctions f définies sur R par : f (x) = ke½x −8, avec k réel.
Solution générale de y' -0,5y = 0 : f(x) =k e0,5x avec k une constante réelle.
Solution particulière de (E) : g(x) = -8.
Solution générale de (E) : f(x) = ke½x −8
Affirmation vraie.

 2. Dans une classe de terminale, il y a 18 filles et 14 garçons. On constitue une équipe de volley-ball en choisissant au hasard 3 filles et 3 garçons.
Affirmation 2 : Il y a 297 024 possibilités pour former une telle équipe.
Il y a (183) =  18 x17 x16 /(2 x3 ) =816 façons de choisir 3 filles parmi 18 filles.
Il y a (143) =  14 x13 x12 /(2 x3 ) =364 façons de choisir 3 garçons parmi 14 garçons.
816 x364=297 024 possibilités.
 Affirmation vraie.

  3. Soit (vn) la suite définie pour tout entier naturel n par : vn = n / (2+cos(n))
 . Affirmation 3 : La suite (vn) diverge vers +∞.
-1 < cos(n) < 1.
1 <2+ cos(n) < 3.
vn tend vers +oo si n tend vers +oo.
Affirmation vraie.

4. Dans l’espace rapporté à un repère orthonormé  on considère les points A(1; 1; 2), B(5 ; −1 ; 8) et C(2; 1; 3).
 Affirmation 4 :

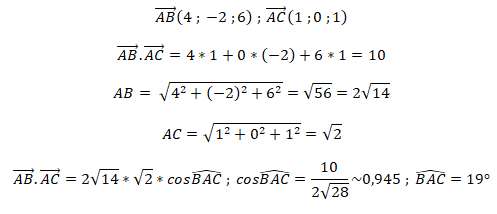Affirmation fausse.

  5. On considère une fonction h définie sur ]0 ; +∞] dont la dérivée seconde est définie sur ]0 ; +∞] par : h ′′(x) = x ln(x) −3x. Affirmation 5 : La fonction h est convexe sur [ e 3 ; +∞[.
Le signe de h"(x) est celui de ln(x) -3.
Si x appartient à [e3 ; +oo[ : e3 < x.
ln(e3) < ln(x) car ln est croissante sur R*+.
3 < ln(x) ; 0 < ln(x)-3.
0 < h"(x). La fonction h est convexe sur [ e 3 ; +∞[.
Affirmation vraie.

... =  =
....

 1. Soient E et F les ensembles E = {1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7} et F = {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}.
Affirmation 1 : Il y a davantage de 3-uplets d’éléments distincts de E que de combinaisons à 4 éléments de F.
Les 3-uplets d’éléments distincts de E sont des arrangements de 3 éléments distincts  choisis parmi 7. Il y en a  : 7! /(7-3)! =7 x6x5 =210.
Nombre de combinaisons à 4 éléments de F : (104) =10 x9x8x7 / (2x3x4)=210.
Affirmation fausse.

 2. Dans le repère orthonormé  on a représenté la fonction carré, notée f , ainsi que le carré ABCD de côté 3.

Affirmation  2 : La zone hachurée et le carré ABCD ont la même aire.
Aire du carré : 3 x3 = 9 unités d'aire.
Aire hachurée :
Affirmation vraie.

3. On considère l’intégrale J ci-dessous :

. Affirmation  3 : Une intégration par parties permet d’obtenir : J = 7 /11 .
On pose u '= x et v = ln(x)  ; u = ½x2 ; v' = 1 /x.

7 / 11 ~0,63636.
Affirmation fausse.

 4. Sur R, on considère l’équation différentielle (E) : y ′ = 2y −e x .
Affirmation 4 : La fonction f définie sur R par f (x) = e x + e 2x est solution de l’équation différentielle (E).
f '(x) = ex+2e2x. Repport dans (E) :
ex+2e2x =2 e x +2 e 2x -ex=e x +2 e 2x.
Affirmation vraie.

 5. Soit x donné dans [0; 1[. On considère la suite (un) définie pour tout entier naturel n par : un = (x −1)en +cos(n).
Affirmation 5 : La suite (un) diverge vers −∞.
-1 < cos(n) < 1.
x-1 < 0.
en tend vers + oo si n tend vers +oo.
(x −1)en tend vers -oo.
Par somme des limites, un tend vers -oo.
Affirmation vraie.



  
menu