Physique chimie : étude d'un orgue ancien. Bac SPCL 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Etude
d'un orgue ancien.
PARTIE A – Accordage de l’orgue.
Au cours du temps, un orgue peut se dérégler. Les sons émis ne
correspondent plus aux
bonnes notes : l’orgue est alors désaccordé. Il est alors nécessaire de
réaliser un accordage.
Pour cela, on compare une note jouée à l’orgue et la note de référence
émise par un diapason.
On règle la note de l’orgue jusqu’à ce qu’elle ait la même fréquence
que celle du diapason.
Q1. Donner la
condition nécessaire, lorsqu’un son est émis, pour qu’il puisse se
propager.
Un son correspond à la propagation d'une variation de pression dans
l'air.
Le document suivant présente l’enregistrement d’une note de
l’orgue et d’une autre note jouée au
diapason.
Q2. Justifier que
le signal sonore émis par l’orgue est un son complexe.
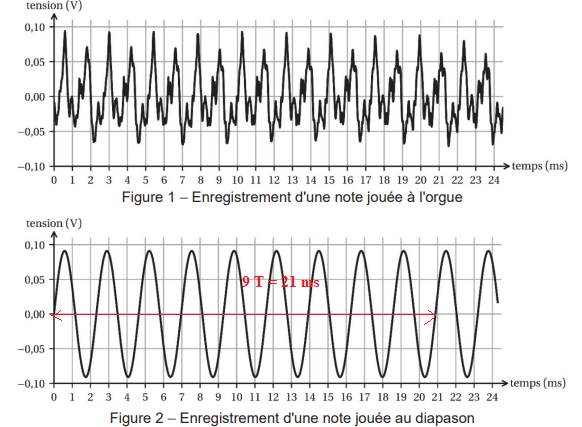
Le signal n'est pas sinusoïdal. Il est composé de plusieurs fréquences
qui se superposent.
Q3. Montrer que la
période de la note émise par le diapason vaut T = 2,33 ms, en
expliquant la démarche permettant d’avoir la plus petite incertitude
possible.
9T = 21 ms ; T = 2,33 ms.
Cet orgue doit servir pour jouer des œuvres anciennes. Afin d’être le
plus fidèle possible à
l’œuvre originale, la note de référence doit être la même que celle
utilisée à l’époque de la
composition des morceaux. Un diapason différent est utilisé pour chaque
année mentionnée :
Diapason
|
1
|
2
|
3
|
4
|
5
|
Année
|
1680
|
1774
|
1807
|
1829
|
1955
|
fréquence
de référence (Hz)
|
404
|
410
|
420
|
430
|
440
|
Q4. Déduire de la question
précédente à quelle année de composition correspond le
diapason.
f = 1 / T =1 /(2,33 10-3)=429
Hz. Année 1829.
Le système qui permet d’accorder les tuyaux à anches est présenté.
Constitution d’un tuyau à anches
Pour produire un son, la languette est plaquée contre
l’anche mais ne l’obstrue pas totalement. Cela permet à
l’air de faire vibrer la languette et de produire le son.
La rasette permet d’accorder le tuyau :
si on enfonce la rasette, cela diminue la longueur de
la languette et rend le son plus aigu ;
si on remonte la rasette, on augmente la longueur de
la languette et rend le son plus grave.
La fréquence de la note
jouée par l’orgue vaut f = 417 Hz.
Q5. Expliquer la
manipulation à réaliser sur la rasette pour que le tuyau d’orgue émette
la
même note que le diapason.
417 Hz < 429 Hz ; il
faut augmenter la fréquence, donc rendre le son plus aigu : il
faut enfoncer la rasette.
PARTIE B – Mesure et effet
de la température sur le son de l’orgue.
En plus des tuyaux à anches vus dans la partie A, un orgue est
également constitué de tuyaux
à bouche. On étudie l’influence de la température sur le
son émis par ces tuyaux.
On modélise un tuyau à bouche par un tuyau de longueur L ouvert à une extrémité et fermé à
l’autre, dans lequel s’établit une onde sonore stationnaire.
Le mode fondamental (n = 0) de l’onde correspond à la plus basse fréquence f0 et les
harmoniques de rang n correspondent aux autres modes. La longueur d’onde de l’harmonique
de rang n est donnée par la relation :
ln = 4L/(2n+1).
Q6. Donner l’expression de la longueur d’onde l0 du mode fondamental en fonction de la
longueur L du tuyau.
l0 = 4L
Q7. Montrer que la fréquence f0 du son produit s’écrit, en fonction de la longueur L du tuyau
et de la célérité du son cson, sous la forme :
f0 = cson
/(4L).
f0 = cson
/ l0 = cson
/(4L).
Un orgue est constitué de tuyaux à bouche de différentes longueurs afin de produire des sons
plus ou moins aigus.
Q8. Déduire de la relation précédente que les tuyaux les plus courts permettent de produire
les sons les plus aigus
Les fréquences des sons aigus sont les plus élevées : les tuyaux doivent donc être les plus courts.
À une température de 15 °C, la célérité cson du son a pour valeur 340 m / s.
Q9. Montrer que pour émettre un son de fréquence f0 égale à 121 Hz, à cette température,
un tuyau à bouche doit avoir une longueur de l’ordre de L = 70 cm.
4 L = cson
/ f0 =340 / 121=2,81 m ; L = 2,81 / 4 =0,70 m = 70 cm.
Il a été constaté que le son de l’orgue varie selon les saisons.
En effet, la dépendance de la célérité cson du son dans l’air avec la température
T (en K) peut être modélisée par la relation :
cson = 20,03 × T½.
Q10. Montrer que la fréquence fondamentale f0 du tuyau étudié à la question précédente
est liée à la température T de l’air par la relation : f0 = 7,2 ×T½.
.
f0 = cson
/ l0 = cson
/(4L)= 20,03 × T½/ (4 L) =20,03 × T½/ 2,81= 7,2 ×T½.
.
Pour vérifier la validité du modèle, on étudie au laboratoire la variation de la fréquence
fondamentale du son émis dans un tuyau en fonction de la température de l’air.
On produit dans le tuyau une onde
sonore, dont la fréquence est réglée
par un générateur. En faisant varier la
fréquence, on peut déterminer la
fréquence fondamentale f0 pour
laquelle l’amplitude mesurée à
l’oscilloscope est maximale.
La température de l’air dans le tuyau est modifiée grâce à un fil chauffant. Une sonde de
température (B) de type Pt100 permet de la mesurer.
Caractéristique de la sonde Pt100 :
R = 0,385 × q + 100 avec R la résistance (en ohm) et ș la température (en °C).
Lors d’une mesure, la valeur de la résistance de la sonde Pt100, mesurée à l’ohmmètre, est
de 115 ohms.
Q11. Calculer la température q de l’air dans le tuyau.
115 = 0,385 × q + 100 ; q = 15 /0,385 =39°C.
On réalise plusieurs mesures à des températures différentes, puis on trace le graphique de la
fréquence fondamentale mesurée en fonction de T½ (exprimée en K½).
Q12. Expliquer pourquoi, pour valider la relation f0 = 7,2 × T½, on peut réaliser une
modélisation linéaire des points expérimentaux.
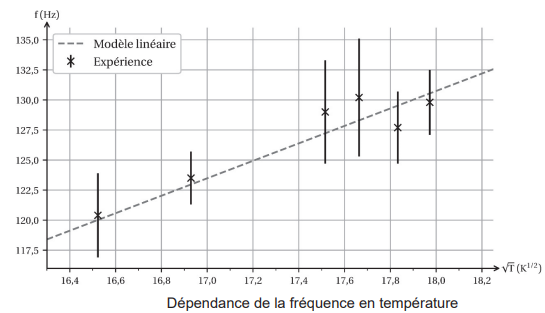
Les points sont pratiquement alignés sur une droite ne passant pas par l'origine ( fonction affine).
Entre l’été et l’hiver, la température de l’air dans le tuyau passe de 23 °C à 10 °C.
Le point
correspondant à la température moyenne en hiver est placé.
Q14. Placer précisément le point correspondant à la température en été sur la courbe de la
modélisation du
273+23 = 296 ; 296½ =17,2.
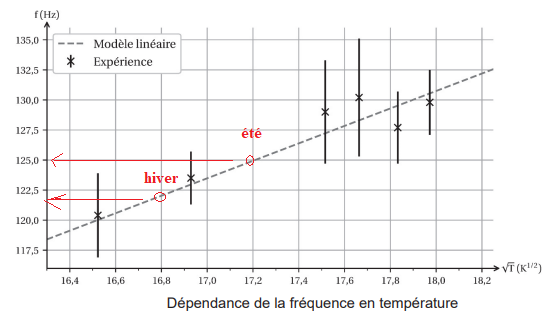
Q15. Vérifier que le son est plus aigu en été.
En hiver : 122 Hz ; en été ; f = 125 Hz, lz son est plus aigu.
PARTIE C – Numérisation d’une mélodie.
On souhaite effectuer des enregistrements sonores des notes de l’orgue. La numérisation est
effectuée par un Convertisseur Analogique Numérique (CAN). Les informations numérisées
seront stockées sur une clé USB.
Données : caractéristiques des deux CAN disponibles.
CAN 1 : 12 bits ; période d'échantillonnage Te = 5,0 µs ; plage de conversion DU = 10 V.
CAN 2 : 8 bits ; période d'échantillonnage Te = 5,0 µs ; plage de conversion DU = 10 V.
Q16. Calculer la valeur de la fréquence fe d’échantillonnage des deux CAN.
fe = 1 / Te = 1 /(5,0 10 -6)=2,0 10 5 Hz = 200 kHz..
Pour numériser un signal, la fréquence d’échantillonnage fe doit vérifier le critère de Shannon :
fe > 2 × f max
où f max est la plus haute fréquence présente dans le signal analogique.
On souhaite numériser des sons audibles pour les êtres humains, c’est-à-dire de fréquences
comprises entre 20 Hz et 20 kHz.
Q17. Justifier que la valeur de la fréquence fe d’échantillonnage des deux CAN est adaptée
pour numériser ces sons.
2 f max = 40 kHz ;
fe > 2 × fmax .
Le quantum d’un CAN est donné par la relation suivante :
q = DU/
(2 N-1) ; q : quantum (V) ; DU : plage de conversion (V);
N : nombre de bits.
Q18. Parmi les deux CAN proposés, déterminer celui qui reproduira un signal numérique le
plus fidèle au signal analogique.
CAN 1 : q = 10 /(2 12-1)= 2,44 10 -3 V.
CAN 2 : q = 10 /(28-1)= 3,9 10-2 V.
Le CAN 1 est retenu.
La taille d’un fichier audio enregistré sur un seul canal, exprimée en bit, est donnée par la
relation suivante :
Taille =
N × Dt/
Te
; N : nombre de bits du CAN
; Dt : durée d’enregistrement (s)
Te : période d’échantillonnage (s)
Le CAN retenu est utilisé pour numériser le signal d’une mélodie de 61 secondes.
Q19. Montrer qu’une clé USB possédant 50 Mio d’espace libre peut être utilisée pour stocker
le fichier.
1 Mio=1024 kio ; 1 kio = 1024 octets.1 octet = 8 bits.
Taille = 12 x61 / (5 10 -6)=1,46 10 8 bits ; 1,46 10 8 /8 =1,83 10 7octets ; 1,83 10 7/1024=1,79 10 4 kio =17,4 Mio.
La clé USB de 50 Mio peut être utilisée.
|
...
= =
|
....
|
PARTIE D – Analyse de l’alliage constituant les tuyaux.
L’alliage utilisé pour la conception des tuyaux d’orgue est uniquement constitué des éléments
plomb Pb et étain Sn. Pour préserver ses qualités mécaniques, l’alliage ne doit pas dépasser
50 % en masse de plomb.
On cherche à déterminer le pourcentage en masse de plomb des tuyaux de l’orgue. Pour cela,
un échantillon de l’alliage issu du tuyau est traité afin d’en extraire les ions plomb (II) Pb2+ par
précipitation sélective. Leur masse est ensuite déterminée par titrage.
Première étape : dissolution de l’alliage.
Dans un erlenmeyer de 500 mL, introduire 0,300 g de l’alliage.
Sous hotte, ajouter 300 mL de solution d’acide nitrique H+aq + NO3-aq.
Sous hotte, porter le mélange à ébullition pendant 5 min puis laisser refroidir.
Lors de l’introduction de l’alliage étain-plomb dans l’acide nitrique il se
produit une transformation de l’étain Sn, modélisée par la réaction d’oxydoréduction
d’équation :
4 NO3
– aq + 3 Sn (s)+ 16 H+ aq+ 4 NO (g) + 8 H2O + 3 Sn4+ (aq)
Q20. Écrire les équations de demi-réaction permettant d’aboutir à l’équation de réaction
précédente.
Sn (s)--> Sn4+ aq +4e-. (E°=0,05 V)
4H+ aq+ NO3
– aq +3e- --> 2H2O(l) + NO(g). (E°=+0,96 V)
Q21. Justifier à l’aide des données que les ions nitrate
peuvent réagir aussi avec le
plomb Pb pour donner l’ion Pb2+.
Pb2+aq / Pb(s) = -0,13 V.
NO3
– aq est l'oxydant le plus fort ; Pb(s) est le réducteur le plus fort.
Deuxième étape : précipitation sélective de l’hydroxyde d’étain.
L’étape suivante consiste à séparer les éléments étain et plomb.
Les ions Sn4+ et Pb2+ précipitent en milieu basique avec les ions HO–
pour former
respectivement l’hydroxyde d’étain Sn(OH)4 (s) et l’hydroxyde de plomb Pb(OH)2 (s).
Q22. Écrire l’équation de réaction modélisant la précipitation de l’hydroxyde d’étain
Sn(OH)4 (s).
Sn4+aq + 4 HO-aq --> Sn(OH)4 (s).
La séparation est réalisée par précipitation sélective de l’hydroxyde d’étain Sn(OH)4 (s).
Le pH initial de la solution issue de la première étape est égal à 0,2.
Dans les conditions de l’expérience, le précipité d’hydroxyde d’étain Sn(OH)4 (s) se forme à
partir d’un pH supérieur à 0,3 et celui d’hydroxyde de plomb Pb(OH)2 (s) à partir d’un pH
supérieur à 7,3.
Q23. Parmi les trois intervalles de pH suivants, indiquer, en justifiant, celui pour lequel la
quasi-totalité des ions Sn4+ a précipité sans qu’il n’y ait de précipitation des ions Pb2+.
La valeur minimale doit être supérieure à 0,3 ; la valeur maximaledoit être inférieure à 7,3.
pH compris entre 2 et 5.
Le protocole utilisé pour la précipitation est donné ci-dessous.
- Verser une solution d’hydroxyde de sodium dans le bécher contenant l’alliage,
jusqu’à atteindre pH = 5.
- Filtrer la solution par gravité.
- Conserver le filtrat pour le dosage des ions Pb2+.
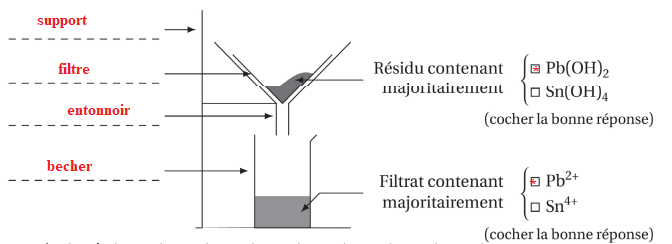
Q24. Compléter le schéma
du dispositif de filtration en nommant le matériel et en précisant la nature des espèces
chimiques majoritairement présentes dans le filtrat et le résidu.
À la suite de l’étape de précipitation sélective, on dispose d’un volume V0 = 400 mL d’une
solution notée S contenant des ions nitrate NO3
–
et tous les ions Pb2+ issus du morceau de
tuyau traité initialement. Le pH de cette solution est maintenu à une valeur de 5.
On titre cette solution.
Titrage des ions plomb (II) par l’EDTA
:
Verser un volume V1 = 40,0 mL de la solution S dans un erlenmeyer de 100 mL.
Ajouter quelques gouttes d’une solution d'orange de xylénol, un indicateur coloré qui
permet de repérer l’équivalence par changement de couleur.
Titrer par une solution d’EDTA de concentration en quantité de matière
C2 = 6,00 × 10–3
mol / L
.
À pH = 5, l’EDTA est sous la forme H2Y2–
et réagit avec les
ions plomb (II) Pb2+ selon l’équation :
Pb2+ aq + H2Y2– aq --> PbY2–
(aq) + 2 H+
(aq).
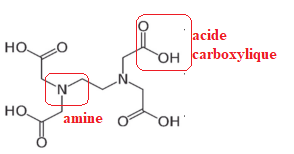
Q25. Nommer les deux fonctions chimiques présentes dans la molécule d’EDTA.
Le volume équivalent obtenu à l’issue du titrage vaut Véq = 11,3 mL.
Q26. Montrer que l’équation support du titrage permet d’établir
que la quantité de matière titrée d’ions Pb2+ est n1 = C2 × Veq.
n(EDTA) = C2 × Veq.
n(Pb2+) =n1=V1[Pb2+].
A l'équivalence : n(Pb2+) =n(EDTA) = C2 × Veq.
Q27. En déduire la valeur de la quantité de matière n1.
n1 = 6,00 10-3 x11,3 =6,78 10-2 mmol.
Soit 0,678 mmol dans 400 mL de solution.
La quantité de matière d’ions plomb (II) Pb2+ dans le volume V0 = 400 mL de solution S est
égale à la quantité de matière de plomb Pb présent dans les 0,300 g de l’alliage traité.
Donnée : masse molaire atomique du plomb M = 207,2 g/ mol.
.
Q28. Montrer, à partir des résultats du titrage du volume V1 = 40,0 mL de solution S, que la
masse de plomb présente dans l’alliage vaut 140 mg.
Q29. En déduire le pourcentage en masse de plomb dans le tuyau et vérifier que cet alliage
convient à la fabrication de tuyaux d’orgue.
0,678 x207,2 =140 mg = 0,14 g de plomb dans 0,300 g d'alliage.
0,14 / 0,300 =0,47 (47 % < 50 %).
Cet alliage convient pour fabriquer les tuyaux d'orgue.
|
|
|
|