Mathématiques,
physique chimie. Bac sti2d 2025
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Partie 1.
L’équipement électrique dont on désire déterminer le facteur de puissance est constitué de l’association d’une bobine, composant électrique présent dans de nombreux circuits électriques, et d’un résistor. On réalise le circuit représenté sur la
figure ci-dessous.
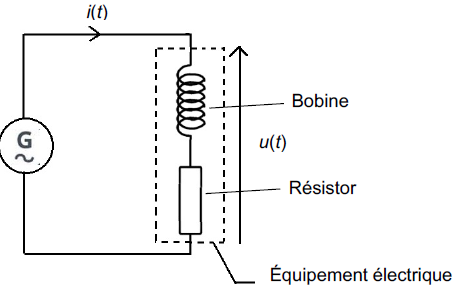
La figure ci-après représente l’évolution temporelle de la tension u(t) aux bornes de l’équipement électrique.
Q1. Déterminer par lecture graphique la valeur maximale, notée Umax, de la tension observée puis calculer la valeur efficace associée, notée Ueff.
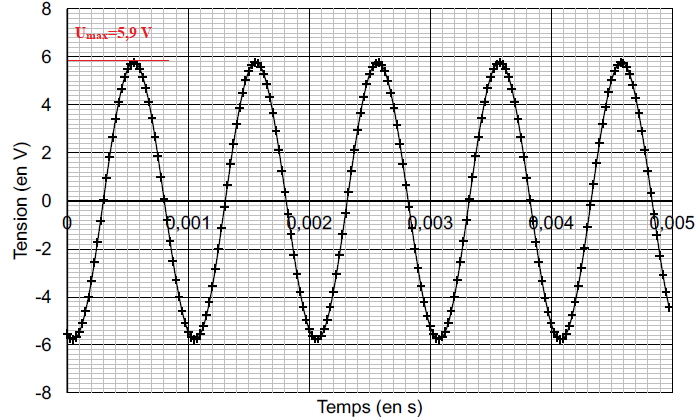
Ueff = Umax / 2½ =4,17 ~4,2 V.
Q2. Sachant que la valeur efficace de l’intensité du courant est égale à Ieff = 3,5×10-3 A, montrer que la puissance apparente S de l’équipement électrique a pour valeur approximative S = 1,4×10-2 VA.
S = Ueff Ieff =4,17 x3,5 10-3~1,4 10-2 VA.
On
rappelle que l’expression du facteur de puissance k en fonction de la
puissance active et de la puissance apparente est : k = P / S..
Q3. Sachant que la puissance active P reçue par l’équipement électrique a pour valeur P = 1,2×10-2 W, calculer son facteur de puissance k.
k = 1,2 10-2/(1,4 10-2)=0,86.
Q4. Montrer que l’énergie E reçue par l’équipement électrique pendant une durée d’une minute a pour valeur E = 0,72 J.
E = P t = 1,2 10-2 x60 =0,72 J.
Q5. On souhaite
diminuer les pertes d’énergie induites dans les lignes d’alimentation
par l’utilisation de l’appareil en modifiant son facteur de puissance k
sans changer la puissance électrique qu’il reçoit. Préciser s’il est
nécessaire d’augmenter ou de
diminuer la valeur de k.
Il faut augmenter k.
Partie 2
On établit un modèle numérique à partir de l’expérience décrite en
partie 1. On suppose que la fonction modélisant la puissance
instantanée, exprimée en mW, reçue par l’équipement électrique en
fonction du temps 𝑡, exprimé en seconde, est définie sur l’intervalle
[0;+∞[ par :
f(t) = 12,25 − 13,91 sin (12466 t).
Q6. On considère la fonction F définie sur [0;+∞[ par :
F(t) = 12,25 t + 13,91 / 12466 cos (12466 t).
Montrer que F est une primitive de f sur l’intervalle [0;+∞[.
On dérive F : 12,25 -13,91 sin(12466 t)= f(t).
Q7. L’intégrale Emod =F60)-F(0) modélise l’énergie reçue par l’équipement électrique pendant une minute, exprimée en mJ. Calculer l’énergie Emod, en arrondissant à l’unité.
Emod = 12,25 *60 + 13,91 / 12466 cos (12466 *60) -(13,91 / 12466) =735-5,58 10-4-1,12 10-3=735 mJ.
L’incertitude type sur l’énergie de valeur E = 0,72 J, mesurée à la question Q4, vaut
u(E)=10 mJ. Le nombre z d’incertitudes types qui séparent E et Emod est donné par la
relation :z = |E-Emod| / u(E).
Q8. Calculer la valeur de z et discuter l’accord entre le modèle adopté et la valeur mesurée de E.
z = (735-720) / 10 =1,5 < 2. Donc accord entre les valeurs.
La flamme des jeux olympiques
Le voyage de la flamme olympique depuis son allumage à Olympie en Grèce
jusqu’à la vasque de Paris a été une grande aventure. On s’intéresse
dans cet exercice au fonctionnement de la torche olympique portée par
les relayeurs, puis au lancement de la grande vasque olympique dans le
ciel parisien.
Partie 1 – La flamme olympique
Il y a en réalité deux flammes olympiques :
- la torche olympique, que portent les relayeurs, soumise aux aléas
météorologiques et susceptible de s’éteindre. Cette torche est
alimentée par une cartouche de gaz propane sous pression qu’il faut
renouveler toutes les 8 minutes ;
- la lanterne olympique, qui est protégée par une vitre et manipulée
par des officiels. La lanterne est composée d’une mèche trempant dans
un réservoir de paraffine qui sert de combustible.
Dans cette partie, on se propose de comparer les propriétés de ces deux dispositifs.
Donnée : la formule chimique brute du propane est C3H8.
Q1. Écrire l’équation de la réaction de combustion complète du propane par le dioxygène de l’air.
C3H8 + 5O2 --> 3 CO2 + 4H2O.
On cherche à évaluer le pouvoir calorifique de la combustion de la paraffine. Pour cela, on introduit un volume d’eau Veau à la température initiale q i = 21,3°C dans une canette de soda dans laquelle on place un thermomètre.
Une bougie allumée, composée de paraffine, de masse mi est placée sous la canette.
Au bout de quelques minutes, on éteint la bougie et on relève la température finale de l’eau q f contenue dans la canette ainsi que la masse finale de la bougie mf.
Données :
- pouvoir calorifique du propane : 12,8 kWh·kg-1 ;
- masse volumique de l’eau liquide : ρeau= 1,00 g·mL-1 ;
- volume de l’eau contenue dans la canette de soda : Veau = 100 mL ;
- capacité thermique massique de l’eau liquide : ceau = 4,18×103J·kg-1·K-1 ;
- température initiale de l’eau : q i = 21,3°C ;
- température finale de l’eau : q f = 44,5°C ;
- masse initiale de la bougie : mi = 11,74 g ;
- masse finale de la bougie : mf = 11,43 g ;
- on rappelle : 1kWh = 3,6×103 kJ.
Q2. Montrer que l’énergie thermique reçue par l’eau contenue dans la canette pendant cette expérience vaut Eth = 9,70 kJ.
Eth =Veau ρeauceau(q f -q i)=100x4,18 (44,5-21,3)=9,7 103 J = 9,7 kJ.
Q3.
En supposant que l’énergie libérée par la combustion de la paraffine
est intégralement transmise à l’eau contenue dans la canette, montrer
que le pouvoir calorifique de la paraffine mesuré par cette expérience
vaut approximativement
PC = 3,13×104 kJ·kg-1.
Msse de parafine brûlée = 11,74-11,43 =0,31g = 3,1 10-4 kg.
PC =9,7 / (3,1 10-4) =3,13×104 kJ·kg-1.
Q4. Le pouvoir calorifique de la paraffine publié dans la littérature scientifique est de l’ordre de 4,0×104 kJ·kg-1.
Proposer une explication de l’écart observé entre la valeur
expérimentale calculée à la question Q4 et la valeur publiée dans la
littérature
scientifique.
Pertes de chaleur ( métal, air) et combustion incomplète expliquent l'écart.
Q5. Comparer la valeur du pouvoir calorifique de la paraffine à celle du pouvoir
calorifique du propane et conclure quant à la pertinence du choix du
propane pour faire fonctionner la torche soumise aux aléas
météorologiques.
le pouvoir calorifique du propane est supérieur au pouvoir calorifique de la parafine.
Partie 2 – La vasque olympique
La vasque olympique de Paris était constituée d’un grand ballon captif, gonflé à l’hélium, transportant une nacelle.
L’ensemble {ballon + nacelle} était attaché à un câble vertical, relié au sol, qui accompagnait le mouvement de la vasque
pendant son ascension. Afin d’étudier le mouvement d’ascension, supposé
vertical, de la vasque dans le ciel parisien, on a réalisé un pointage
de ses positions successives au cours du temps.
Le graphique indiquant l’altitude de la vasque en fonction du temps est donné en figure ci-après.
Le système {ballon + nacelle}, assimilable à un point matériel, est soumis aux forces suivantes :
- le poids P ;
- la poussée d’Archimède exercée par l’air, notée F, de même direction que le poids P et de sens opposé ;
- la force de tension du câble qui retient le système, notée T, de même direction que la vitesse du ballon et de sens opposé.
Q6. En utilisant le
graphique de la figure , montrer que l’on peut considérer que la
vitesse du système {ballon + nacelle} est constante lors de son
ascension.
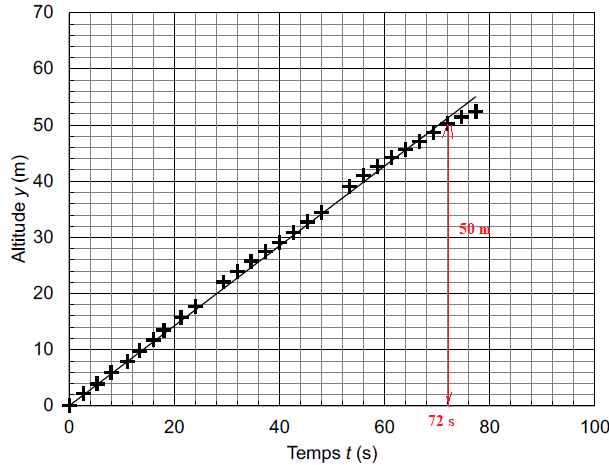
Le graphe est une droite passant par l'origine.
Q7. Déterminer la valeur de la vitesse du système {ballon + nacelle} au cours de l’ascension.
v = 50 / 72 ~0,69 m /s.
Q8. Sachant que la
durée totale de l’ascension de la vasque olympique était 1 min 30
s, déterminer l’altitude de la vasque à la fin de son ascension.
0,69 x(60+30)=62,5 m.
Q9. Montrer que l’accélération du système {ballon + nacelle} est nulle lors de l’ascension.
L'accélération est égale à la dérivée de la vitesse par rapport au temps. la vitesse étant constante, l'accélération est nulle.
Données :
- masse du système {ballon + nacelle} : m = 2300 kg ;
- intensité de la pesanteur : g = 9,8 N·kg-1.
Q10. Déterminer la valeur du poids de l’ensemble {ballon + nacelle}.
P = mg = 2300 x9,8 =2,25 104 ~2,3 104 N.
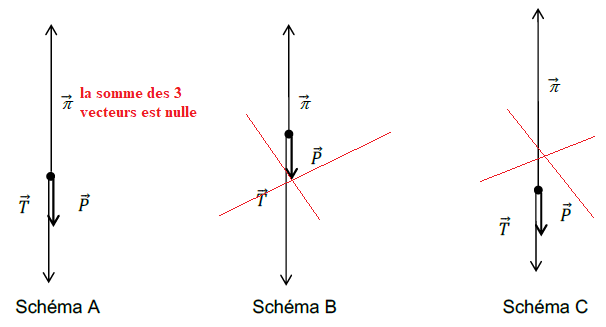
Q11. À partir du
résultat de la question Q9 et du principe fondamental de la dynamique,
indiquer celui des trois schémas de la figure qui représente de
manière correcte les différentes forces appliquées à l’ensemble {ballon
+ nacelle} au cours de l’ascension verticale de la vasque.
|
...
= =
|
....
|
Mathématiques.
Question 1. On considère le point M représenté dans le plan complexe ci-dessous.
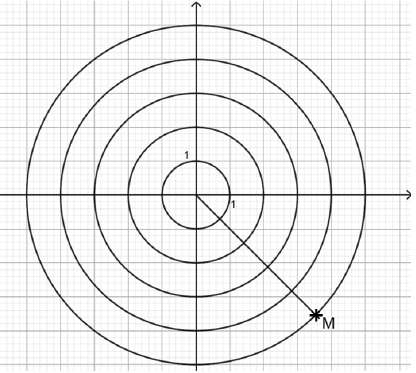
L’affixe du point M est :5 exp(-ip/4).
Question 2
Soit l’équation différentielle y' = 2y − 0,5.
1. Déterminer l’ensemble des fonctions définies sur R qui sont solutions de cette équation.
Solution générale de y'-2y=0 : y = A exp(2x) avec A une constante réelle.
Solution particulière : y = 0,25.
Solution générale : y = A exp(2x) +0,25.
2. Déterminer la fonction f, solution de cette équation, avec pour nombre dérivé f '(0) =-3.
f''(x) = 2A exp(2x) ; f '(0) = 2A= -3. ; A = -1,5
f (x) = -1,5 exp(2x)+0,25.
Question 3
On considère la fonction f définie sur R par f(x) = exp(-0,016x)-2.
Résoudre dans R l’équation f(x) = 0. Donner la valeur exacte de la solution puis une valeur approchée à 10 % près.
exp(-0,016x) = 2 ; -0,016 x = ln(2) ; x = - ln(2) / 0,016 ~ -43.
Question 4
Montrer que, pour tout 𝑥 > 0, l’égalité suivante est vraie :
ln(x4/9) -3 ln(x) +ln(9/x) =0.
3ln(x) = ln(x3 ) ;
ln(x4/9) -3 ln(x)=ln(x4 / (9 x3) )= ln(x / 9).
ln(x4/9) -3 ln(x) +ln(9/x) =ln(x/9)+ln(9 / x) = ln(9x / (9x)) = ln(1) = 0.
Au coeur d’un réacteur nucléaire
Actuellement, près de 65% de l’électricité produite en France est issue
de centrales nucléaires. À l’intérieur de ces centrales, des réacteurs
nucléaires produisent chacun une puissance électrique comprise entre
900 MW et 1450 MW.
Ces réacteurs utilisent la même technologie : de l’eau sous pression
sert à transporter vers le générateur de vapeur l’énergie produite par
les réactions nucléaires. Cet exercice propose d’étudier certains
aspects du fonctionnement d’un réacteur nucléaire.
Partie 1 – Étude du combustible
Le combustible nucléaire présent dans le coeur du réacteur est constitué de dioxyde d’uranium, de formule UO2.
L'élément chimique uranium de symbole U, a pour numéro atomique 92.
L'uranium naturel existe sous la forme de trois isotopes : l'uranium
238, le plus abondant, l'uranium 235 et l'uranium 234. Dans le
combustible nucléaire la proportion en masse d’uranium 235 doit être
comprise entre 3% et 5%.
Données :
Une tonne d’uranium naturel contient :
- une masse m234 = 0,056 kg d’uranium 234 ( 23492U);
- une masse m235 = 7,1 kg d’uranium 235 ( 23592U)
- une masse m238 = 992,8 kg d’uranium 238 ( 23892U)
Q1. Montrer que la
proportion d’uranium 235 dans l’uranium naturel est insuffisante pour
le combustible nucléaire. Celui-ci doit donc être enrichi.
7,1 / 1000 = 7,1 10-3 kg/ tonne soit 0,71 % < 3 %. .
Par bombardement de neutrons, l’uranium 235 est le siège d’une
transformation nucléaire libérant une grande quantité d’énergie.
L’équation de réaction modélisant la transformation est la suivante :
10n+23592U--> 9438Sr+14054Xe+210n. (A)
Q2. À partir de l’équation de réaction (A), indiquer s’il s’agit d’une réaction de fission ou de fusion. Justifier la réponse.
Réaction de fission de l'uranium 235 conduisant au strontium et au xénon.
Données :
- défaut de masse associé à la réaction (A) : Dm = 2,39×10-28 kg ;
- célérité de la lumière dans le vide : c = 3,00×108 m∙s-1.
Q3. Montrer que l’énergie DE libérée lors de cette réaction nucléaire par le noyau d’uranium 235, vaut approximativement 2,2×10-11J.
DE= Dm c2 = 2,39×10-28 x 9,00 1016 ~ 2,2×10-11J.
Données :
- 1 kg de combustible UO2 contient 70 g d’Uranium 235 ;
- masse d’un noyau d’uranium 235 : m( 23592U) = 3,90×10-25 kg .
Q4. Calculer le nombre de noyaux d’uranium 235 contenus dans 1 kg de combustible UO2.
0,070 / (3,90×10-25 ) =1,8 1023.
Q5. En déduire l’énergie libérée par la réaction (A) par kg de combustible UO2.
Comparer la valeur obtenue au pouvoir calorifique du propane qui vaut 4,6×107 J∙kg-1.
1,8 1023 x 2,2×10-11=3,9 1012 J kg-1.
Soit environ 105 fois plus grand que le pouvoir calorifique du propane. Le combusrible nucléaire est très énergétique.
Partie 2 – Assemblage de combustible
Dans le coeur du réacteur se trouvent des assemblages de combustible.
Chaque assemblage comporte 264 « crayons » combustibles composés chacun
d’une gaine qui entoure un empilement de pastilles de dioxyde d’uranium
UO2.
Données :
- le réacteur nucléaire étudié est composé de 157 assemblages de combustible ;
- le volume de combustible dans chaque assemblage est égal à V = 5,1×10-2 m3.
Q6. Calculer la
puissance P dégagée par l’ensemble du combustible dans ce réacteur,
sachant que la puissance dégagée par unité de volume de combustible est
de l’ordre de 4,0×108 W·m-3.
Volume total du combustible : 0,051 x157 ~8,0 m3.
Puissance : 8,0 x4,0 108=3,2 109 W =3200 MW.
Ce réacteur permet de produire une puissance électrique Pe = 1100 MW.
Q7. Exprimer puis calculer le rendement de ce réacteur nucléaire.
Puissance électrique / puissance thermique = 1100 / 3200 ~0,34 (34 %).
Partie 3 – Pression de l’eau contenue dans la cuve du réacteur
Dans le coeur du réacteur, l’assemblage de combustible est plongé dans
une cuve contenant de l’eau liquide. Cette eau permet de réguler la
transformation nucléaire et d’assurer les échanges d’énergie dans le
réacteur.
L’eau liquide entre dans la cuve à une température de l’ordre de 190°C
et en ressort à environ 325°C après avoir reçu l’énergie thermique
produite par la transformation nucléaire. Pour qu’elle reste liquide
dans la cuve, l’eau se trouve sous une pression constante P = 155 bar.
La figure ci-dessous représente le diagramme d’état (P,T) de l’eau.
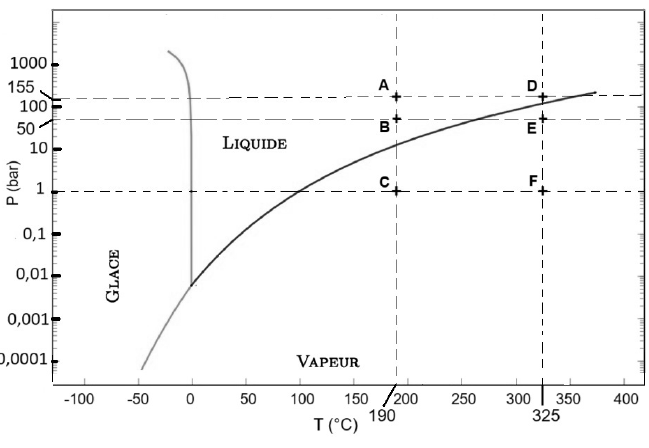
Q8. Justifier que
le chauffage de l’eau dans la cuve est représenté par une transition du
point A au point D sur le diagramme d’état (P,T) de l’eau.
A(190 °C ; 155 bar) ; D(325°C ; 155 bar).
Q9. Expliquer pourquoi le réchauffement de l’eau liquide de 190 °C à 325 °C ne peut pas être réalisé à une pression de 50 bar.
L'eau est à 'état gazeux siT = 190°C et P = 50 bar.
Partie 4 – Protection du combustible
Pour des raisons de sécurité, le combustible nucléaire ne doit pas être
en contact avec le reste du réacteur. La gaine qui entoure le crayon
combustible est constituée d’un alliage appelé zircaloy, choisi pour sa
résistance à la corrosion.
Dans la cuve, le zirconium Zr présent dans le zircaloy réagit avec l’eau qui l’entoure.
Une réaction d’oxydoréduction se produit et conduit à la formation d’un
oxyde de zirconium sur la surface de la gaine. Cette couche d’oxyde est
imperméable à l’eau.
Les demi-équations des couples d’oxydoréduction mis en jeu au cours de cette transformation chimique sont :
ZrO2 (s) + 4 H+(aq) + 4e- = Zr (s) + 2 H2O (ℓ)
H2O (ℓ) + 2 H+(aq) + 2e- = H2 (g) + H2O (ℓ)
Q10. Indiquer si le zirconium Zr(s) présent dans la gaine est un oxydant ou un réducteur. Justifier.
ZrO2 (s) gagne des électrons ; c'est un oxydant qui se réduit : Zr() est le réducteur du couple ZrO2 (s) / Zr(s).
Q11. Écrire l’équation de la réaction d’oxydoréduction se produisant entre le zirconium Zr(s) et l’eau.
Zr (s) + 2 H2O (ℓ)-- >ZrO2 (s) + 4 H+(aq) + 4e-
2H2O (ℓ) + 4 H+(aq) + 4e- = 2H2 (g) + 2H2O (ℓ).
Ajouter et simplifier :
Zr (s) + 2 H2O (ℓ)-- >ZrO2 (s) + 2H2 (g).
Q12. Expliquer pourquoi la couche d’oxyde de zirconium formée à la surface de la gaine permet de la protéger de la corrosion.
La couche de ZrO2 est solide stable et imperméable à l'eau.
De plus ZrO2 est un oxydant.
|
|
|
|