Mathématiques,
physique chimie. Bac sti2d 2025
Polynésie.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Accélération d'un véhicule.
Un véhicule électrique de masse, notée M, de valeur 1 600 kg, se déplace sur une
route horizontale et rectiligne.
Le constructeur souhaite vérifier si l’intensité de la force F de traction vaut environ
800 N pour une accélération de 0,5 m·s- 2.
Le graphique suivant représente l’évolution de la vitesse instantanée v
(exprimée en m⋅s- 1) en fonction du temps t (exprimé en seconde) durant 50 secondes.
1 u.a. = 1 unité d’aire.
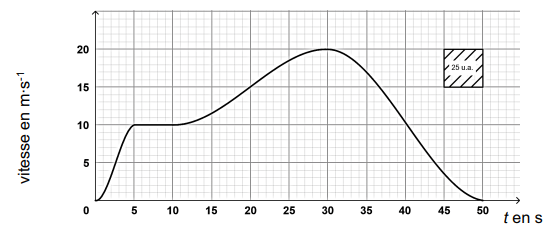
1. Décrire la nature du mouvement de la voiture sur chacun des intervalles de temps
[0 ; 5], [5 ; 10], [10 ; 30] et [30 ; 50].
On s’intéresse à l’accélération instantanée du véhicule sur l’intervalle [1 ; 4], et on
admet que sur cet intervalle, on a : v(t) = 2t.
[0 ; 5]: la vitesse croît linéairement, mouvement uniformément accéléré.
[5 ; 10] : vitesse constante, mouvement uniforme.
[10 ; 30] : la vitesse augmente, mouvement accéléré.
[30 ; 50] : la vitesse décroît, mouvement décéléré.
2. Déterminer la valeur de l’accélération a(t) sur l’intervalle [1 ; 4].
v(t) = 2t ; a = 2 m s-2.
La distance totale, notée D et exprimée en mètre, parcourue par le véhicule en 50
secondes est donnée par :
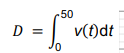
3. Donner, en exploitant le graphique, une estimation de la distance totale
parcourue par le véhicule.
D= aire comprise entre la courbe et l'axe horizontal :
23 carreaux soit 23 x 25 =575 u.a.
4. Déduire la valeur de la vitesse moyenne du véhicule, exprimée en km·h-1, dans
l’intervalle de temps [0 ; 50].
575 / 50 =11,5 m /s ou 11,5 x3,6 =41,4 ~41 km / h.
5. Établir l’inventaire des forces qui agissent sur le véhicule lorsqu’il est en
mouvement.
Poids du véhicule, action de la route et force motrice due au moteur.
On admet que le principe fondamental de la dynamique se réduit ici à la
relation F = ma, où F est la force de traction du véhicule et a l'
accélération.
6. Indiquer la force négligée dans cette étude.
Force de frottement.
Dans l’intervalle de temps [15 ; 25], l’accélération du véhicule a pour norme 0,5 m·s-2.
7. Vérifier si l’intensité de la force F de traction pour une accélération de 0,5 m s-2 vaut environ 800 N sur l'intervalle [0 ; 25].
F = Ma = 1600 x0,5 = 800 N.
Préserver son audition.
Un spectateur se rend à un concert en plein air et souhaite profiter
du spectacle tout en préservant son audition.
Il se demande s’il doit porter des protections auditives ou se placer le plus loin possible
de la scène afin de ne pas s’exposer à des niveaux sonores supérieurs à 90 dB.
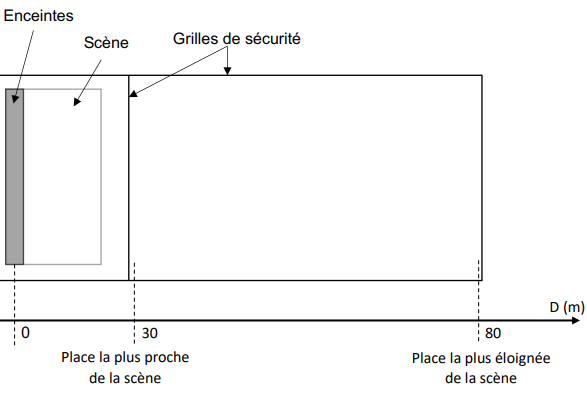
Dans un premier temps, on souhaite vérifier si le niveau sonore, lorsque l’on s’éloigne
au maximum de la scène, respecte la limite de 90 dB.
Pour cela, une expérience est réalisée : on émet un son puis, sans modifier ses
caractéristiques, on trace l’évolution de son intensité sonore en fonction de l’inverse
du carré de la distance à la source sonore.
Liste du matériel disponible.
• Générateur basses fréquences (GBF)
•
Haut-parleur
• Sonomètre
•
Ordinateur muni d’un tableur-grapheur
• Mètre ruban de 10 m
• Oscilloscope
• Microphone.
L'ensemble du matériel proposé n’est pas
nécessairement utilisé.
1. Proposer, à l’aide du matériel listé, un protocole
permettant d’obtenir le graphique ci-dessous.
Emission du son : générateur basse fréquence, haut-parleur :
Réception du son : microphone, ordinateur muni d'un tableur grapheur.
Mesure de distance :mètre ruban.
L’intensité sonore mesurée à 40 cm de la source est de 18,6 × 10–6 W·m-2.
2. Ajouter cette mesure sur le graphique.
1 / 0,42 = 6,25.
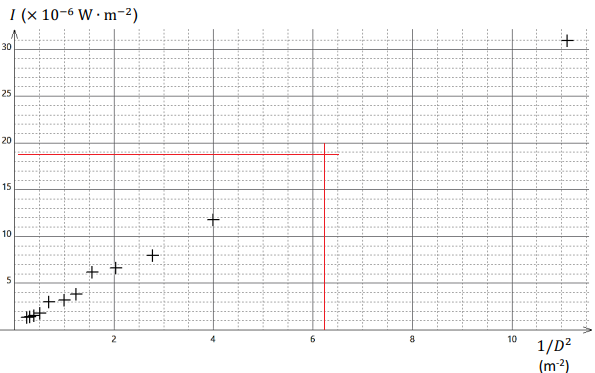
3. Décrire l’évolution de l’intensité sonore en fonction de l’inverse du carré de la
distance, notée D, à la source .
Les points sont alignés sur une droite passant par l'origine.
L'intensité sonore est proportionnelle à 1 /D2.
Les mesures peuvent être modélisées à
l’aide de la relation :
I = 14,3 /D2.
4. Montrer que le
niveau sonore au plus loin des enceintes est de 93 dB.
D = 80 m ; I = 14,3 / 802 =2,2 10-3 W m-2.
L = 10 log(2,2 10-3 / 10-12)=93 dB.
5. Conclure quant à la nécessité de porter des protections auditives.
Une protection auditive est donc nécessaire.
Dans un deuxième temps, on veut vérifier que les protections auditives peuvent
permettre au spectateur de se placer à n’importe quelle distance de la scène. Pour
cela, on détermine l’atténuation due à un bouchon de la protection auditive.
On réalise l’expérience afin d’obtenir deux
oscillogrammes : un premier sans bouchon et un second avec bouchon.
L’atténuation du niveau d’intensité sonore s’exprime par la relation : A = 20 log (Usans / Uavec)
avec : A exprimée en dB ; Usans exprimée en V, l’amplitude du signal mesurée sans bouchon ;
Uavec exprimée en V, l’amplitude du signal mesurée avec bouchon.
L’atténuation caractérise la baisse du niveau sonore subie par le son qui a été transmis
à travers la protection auditive.
Le document suivant propose les signaux en sortie du dispositif de mesure avec ou sans
protection auditive.
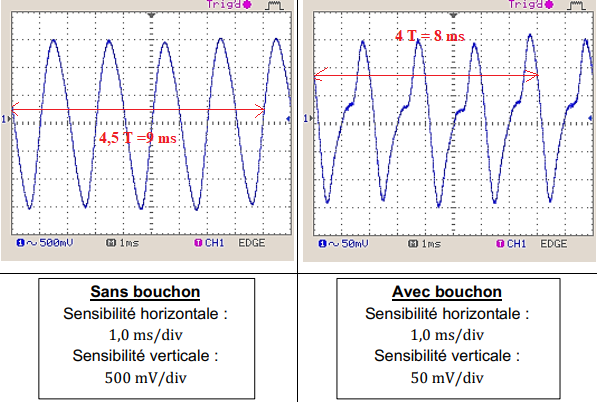
6. Déterminer l’atténuation due à la protection auditive.
A = 20 log( 1,5 / 0,15) =20 dB.
À la place la plus proche de la scène le niveau sonore est de 102 dB.
7. Déterminer le niveau sonore perçu par le spectateur placé juste devant la scène
lorsqu’il porte des protections auditives.
102-20 = 82 dB.
Les protections auditives lui permettent donc de se placer où il le souhaite devant la
scène. Il se demande si les protections auditives ne vont pas modifier le son qu’il
perçoit.
Dans un troisième temps, on souhaite observer les éventuels effets des protections
auditives sur la perception du son.
8. Déterminer la fréquence du son, sans et avec
protection auditive.
Sans protection : T = 9/4,5 = 2 ms ; f = 1 / (2 10-3) =500 Hz.
Avec protection : T = 8 / 4 = 2 ms ; f = 1 / (2 10-3) =500 Hz.
Un enregistrement de la voix d’un chanteur a été réalisé. Il chante un La2 (220 Hz).
Le spectre en amplitude de ce son est représenté :
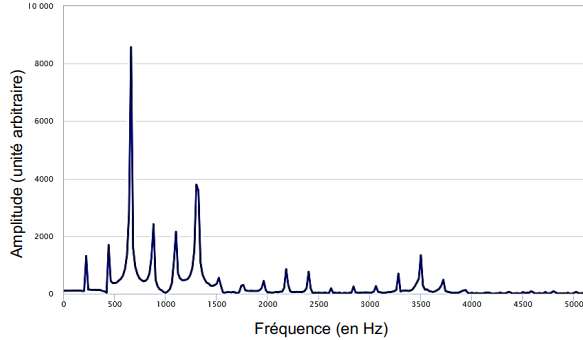
9. Indiquer, en justifiant la réponse, si la voix du chanteur est un son pur ou un son
complexe.
Son complexe : présence de nombreuses harmoniques.
Le dispositif expérimental a permis d’effectuer d’autres
mesures d’atténuation pour la même protection auditive, mais à des fréquences
différentes. Les résultats expérimentaux sont rassemblés dans un tableau.
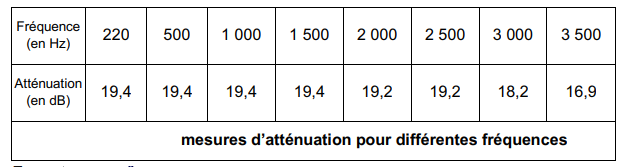
10. Indiquer, en justifiant la réponse, si la voix du chanteur perçue par le spectateur
est modifiée par le port de la protection auditive.
L'atténuation est constante pour des fréquences comprises entre 220 et 1500 Hz : la voix n'est pas modifiée.
L'atténuation n'est pas constante pour des fréquences supérieures à 2000 Hz : la voix est donc modifiée.
|
...
= =
|
....
|
Mathématiques. Partie I
On considère les nombres complexes z1=3½-i et z2 = 2exp(ip/4) où i désigne le nombre
complexe de module 1 et d’argument p/2
.
1. Écrire le nombre z1 sous forme exponentielle. Détailler les calculs.
Module de z1 : (3+1)½=2.
z1 =2( 3½ / 2 -0,5) = 2 (cos (-p/6)+ sin-p/6) = 2 exp(-ip/6).
2. Démontrer que le nombre z = z13 x z22 est un nombre réel en détaillant les calculs.
z = 23 exp(-ip/2) x 4 exp(ip/2)= -23x4 = -32.
Partie II
On considère l’équation différentielle (E) : y' =-4y + 80 où y est une fonction définie
et dérivable sur R et y′ la fonction dérivée de y.
3. Déterminer l’ensemble des solutions de l’équation différentielle (E).
Solution générale de y'+4y = 0 : f(x) = A exp(-4x) avec A une constante réelle.
Solution particulière de (E) : f(x) ) =20.
Solution générale de (E) : f(x) = A exp(-4x) +20.
4. En déduire la solution f de l’équation différentielle (E) qui vérifie f(0) = 100.
f(0) = A+20 = 100 ; A = 80.
f(x) =80 exp(-4x) +20.
5. Donner, sans la justifier, la limite de f en +∞.
exp(-4x) tend vers zéro et f tend vers 20.
Un traitement respectueux de la biodiversité.
Un agriculteur se trouve confronté à la prolifération de plantes vertes dans l’eau de
son étang.
Souhaitant préserver la biodiversité, c’est-à-dire le respect des micro-organismes
(bactéries par exemple), des végétaux et des animaux dans l’étang, il décide de
procéder à une mesure du pH de l’eau.
Il mesure un pH de 5,8. Cette mesure n’est pas conforme aux préconisations
environnementales : il cherche des solutions pour diminuer l’acidité de l’eau de son
étang.
L’agriculteur se demande s’il est préférable d’ajouter de l’eau ou de procéder à un ajout
de carbonate de calcium CaCO3 (s).
Le modèle retenu pour l’étang est assimilé à un
parallélépipède rectangle de volume V = L × ℓ × p (longueur 50,0 m ; largeur 10,0 m ;
profondeur 4,0 m).
1. Nommer l’appareil qui permet la mesure du pH d’une solution.
Le pHmètre.
2. Indiquer pour quelles valeurs du pH une solution est dite acide, neutre ou
basique.
Solution acide : pH < 7 ; neutre pH = 7 ; basique pH > 7.
L’acidité d’une solution est liée à la concentration en ions oxonium H3O+ (aq). En milieu
naturel, la concentration en ions oxonium doit être telle que :
1,1 × 10-7 mol·L< [ H3O+ (aq) ] < 3,2 × 10-7 mol·L. Calculer les pH correspondant à ces deux concentrations limites.
pH = -log(1,1 × 10-7) =6,9 ; pH = -log(3,2 × 10-7) =6,5.
Le document suivant indique, suivant le pH de l’eau de l’étang, le niveau de risques pour
la préservation de la biodiversité.

4. Indiquer, à l’aide du document n°10, la (ou les) plage(s) de valeurs de pH
préconisée(s) pour la préservation de la biodiversité de l’étang.
[6 ; 7 ]
5. Citer les espèces aquatiques en danger si l’eau de l’étang est maintenue à un pH
de 5,8.
Poissons et bactéries.
6. Montrer que la concentration initiale en ions oxonium H3O+ (aq) présents dans
l’étang, notée Ci, vaut 1,6 × 10-6 mol·L-1.
pH = 5,8 ; Ci = 10-5,8 =1,6 × 10-6 mol·L-1.
7. Calculer, en m3 puis en litre, le volume initial de l’étang.
V = 50 x10 x4 =2 000 m3 ou 2,0 106 L.
8. En déduire que la quantité de matière initiale, notée ni, d’ions oxonium présents
dans l’eau de l’étang vaut 3,2 mol.
ni = 2,0 106 x1,6 10-6 =3,2 mol.
L’agriculteur souhaite augmenter la valeur du pH de l’eau de 5,8 à 6,8. Il veut vérifier
préalablement la faisabilité des deux techniques imaginées, c’est-à-dire l’ajout d’eau
dans l’étang ou l’ajout de carbonate de calcium solide CaCO3 (s).
Variation du pH par ajout d’eau dans l’étang.
9. Indiquer le sens d’évolution du pH de l’eau de l’étang lors de l’ajout d’eau,
supposée pure.
Au cours d’une dilution, la quantité de matière du soluté ne varie
pas. Le volume augmente et la concentration en ion oxonium
diminue.
10. Déterminer le volume d’eau final Vf qui permettrait d’atteindre le pH souhaité pour
l’eau de l’étang.
pH = 6,8 ; [H3O+] =10-6,8 =1,585 10-7 mol / L.
1,585 10-7 = 3,2 / Volume total ; Volume total = 2,0 107 L.
Il faut ajouter : 2,0 107 -2,0 106 =1,8 107 L ou 1,8 104 m3.
11. Commenter le résultat obtenu à la question précédente.
Mission impossible, l'étang va déborder.
Variation du pH par ajout de carbonate de calcium solide CaCO3 (s) dans l’eau.
Dans ce domaine de pH (entre 5,8 et 6,8), la réaction entre les ions oxonium H3O+ (aq)
et les ions carbonate CO3
2- (aq) ne conduit pas à une espèce chimique majoritaire.
Donc dans ces conditions, les couples acide / base considérés, sont :
H3O+ (aq) / H2O (ℓ) et HCO3
- (aq) / CO3
2-
(aq).
12. Écrire l’équation-bilan de la réaction acido-basique entre les ions oxonium et les ions carbonate)
H3O+ (aq) +CO3
2-
(aq) --> H2O (ℓ)+HCO3
- (aq).
.
Pour s’approcher du pH souhaité, l’agriculteur doit ajouter une quantité de matière
d’ions carbonate de 3,4 mol, notée n.
On donne également les valeurs des masses molaires :
calcium, MCa = 40,1 g⋅mol-1 ; carbone, MC = 12,0 g⋅mol-1 ; oxygène, MO = 16,0 g⋅mol-1.
13. Calculer la masse m de carbonate de calcium ajoutée à l’eau de l’étang.
M(CaCO3) =40 +12 +3*16=100 g/mol.
m = 3,4 x100 = 340 g.
14. Choisir, en justifiant la réponse, la méthode la plus réaliste pour rectifier l’acidité
de l’eau de l’étang.
Ajout 340 g de carbonate de calcium est réaliste.
|
|
|
|