Mathématiques. DNB Asie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
Exercice 1. 16 points
1 Dans une urne, on dispose de 4 boules bleues, 6 boules violettes, 7 boules rouges, 3 boules jaunes, toutes indiscernables au toucher. On tire une boule au hasard. Quelle est la probabilité d’obtenir une boule violette ?
  6 cas favorables sur 20 possibles : 6 / 20 =3 / 10= 0,3. Proposition C.

 2. Calculer 70 % d’une quantité revient à multiplier cette quantité par : 0,70. Proposition B.

  3. On considère la série suivante composée des 5 valeurs : 7; 18; 12; 13; 15.
Mettre en ordre : 7 ; 12 ; 13 : 15 ; 18.
Etendue : 18-7 =11.
Médiane 13.
Moyenne (7+12+13+15+18) / 5 = 13. Proposition D.

4. Une fonction affine f a pour représentation graphique la courbe ci-dessous. L’expression de la fonction f est :

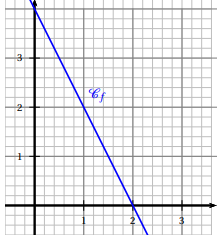
La droite passe par les points de coordonnées (0 ; 4) et (2 ; 0).
y = ax+b ; 4 = 0x+b ; b = 4.
0 = 2a+4 ; a = -2.
f(x) = -2x+4.
Proposition C.

  Exercice 2. 24 points.
Dans la figure ci-dessous qui n’est pas représentée en vraie grandeur :
  Les points G, C et E sont alignés;
 Les points F, C et D sont alignés;
 Les droites (GF) et (DE) sont parallèles.
 Le triangle CDE est rectangle en D
 CD = 21,6cm, CE = 29,1cm, FC = 17,2cm.

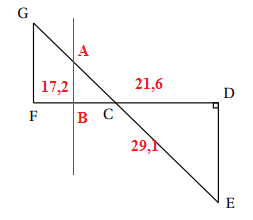1. Montrer que la longueur DE est égale à 19,5cm.
Relation de Pythagore : CE2 = CD2+DE2.
DE2=CE2 - CD2=29,12-21,62 =380,25 ; DE = 19,5 cm.
2. Calculer l’aire du triangle CDE.
DC x DE / 2 = 19,5 x21,6 / 2 =210,6 cm2.
3. Calculer la longueur GF arrondie au millimètre près.
CF / CD = GF / DE ; GF = CF x DE / CD = 17,2 x 19,5 / 21,6 =15,5 cm.
4. On trace une droite (d) perpendiculaire à (FC) avec un logiciel de géométrie dynamique. La droite (d) coupe le segment [GC] en A et le segment [FC] en B. En affichant l’aire du triangle ABC à l’aide du logiciel, on obtient 23,4 cm2 .
a. Montrer que l’aire du triangle ABC est égale à 1/ 9 de l’aire du triangle CDE.
Aire du triangle ABC / aire du triangle CDE = 23,4 / 210,6 =1 / 9.
b. On admet que les triangles ABC et EDC sont semblables. Déterminer la longueur AB.
AB / DE = BC / CD.
AB = BC x DE / CD= BC x19,5 / 21,6~0902 BC.
AB = 0,902 BC ; BC =AB / 0,902.
Aire du triangle ABC : AB x BC / 2 = 23,4 ;
AB x AB /0,902 = 23,4 x2 = 46,8.
AB2 =46,8 x0,902=42,21 ; AB ~6,5 cm.

... =  =
....

 Exercice 3. 20 points.
Dans cet exercice, toutes les longueurs sont exprimées en centimètres. On considère :
 le rectangle ABCD tel que AD = x et AB = 16−2x ;
 le carré EFGH tel que EF = 2x

  PARTIE A : Dans cette partie, x = 1,5 cm.
 1. Calculer le périmètre du carré EFGH.
4 *2x =8 x = 8 *1,5 = 12 cm.
 2. Calculer AB.
16-2x= 16- 3 = 13 cm.
3. Construire en vraie grandeur le rectangle ABCD.

4. Les périmètres de ABCD et EFGH sont-ils égaux ?
Périmètre du rectangle : 1,5 +1,5 +13+13 = 29 cm.
Périmètre du carré : 12 cm.
Les périmètres sont différents.
PARTIE B :
Dans cette partie, on cherche pour quelle(s) valeur(s) de x, le périmètre du rectangle est égal au périmètre du carré.
1. Pour essayer de répondre au problème, on utilise la feuille de calcul suivante :

a. Quel formule a-t-on pu saisir dans la cellule B2 avant de l’étirer jusqu’à G2 ?
=8*B1
 b. Ce tableau nous permet-il de trouver une valeur de x pour laquelle les deux périmètres sont égaux ?
Non.
2. a. Montrer que le périmètre du rectangle peut s’écrire −2x +32.
2(x+16-2x) = 2(16-x)=32-2x.
 b. Déterminer la solution au problème par la résolution d’une équation.
32-2x = 8x.
32 = 10x
x = 3,2 cm.

Exercice 4 : 17 points.
 Dans cet exercice, aucune justification n’est attendue.
Rappel : L’instruction s’orienter à 90 signifie que le lutin se dirige vers la droite.
PARTIE A Un élève souhaite tracer un hexagone à partir de 6 triangles équilatéraux comme sur la figure ci-dessous.

Pour cela, il commence par écrire le script ci-dessous du motif « triangle équilatéral » .
1. Compléter et recopier sur la copie les lignes 2, 3 et 4 du script pour que le lutin dessine un triangle équilatéral de côté 50 pas.

2. Cet élève teste les deux programmes A et B. Il obtient les deux dessins ci-dessous. Quel programme permet de tracer l’hexagone souhaité ?

Programe A.
PARTIE B Un autre élève souhaite tracer un hexagone régulier de 50 pas de côté comme sur la figure ci-dessous :

Sur la copie, recopier le bloc « répéter » en remplaçant A par sa valeur et en le complétant avec 2 instructions choisies parmi les 6 instructions proposées ci-dessous :


Exercice 5 23 points.
 PARTIE A
Un magasin a reçu 650 poissons dont 350 poissons de type A et 300 poissons de type B. La responsable du magasin souhaite vendre ces poissons par lots de sorte que :
 le nombre de poissons de type A soit le même dans chaque lot;
 le nombre de poissons de type B soit le même dans chaque lot;
 tous les poissons soient répartis dans les lots.
1. Parmi les trois propositions suivantes, laquelle correspond à la décomposition en produits de facteurs premiers du nombre 300 ? Aucune justification n’est demandée.
Proposition 1 : 22 x5 x15 ; faux 15 n'est pas premier.
 Proposition 2  : 2 *2*3*5*5 . Vrai.
Proposition 3 : 22 *3*52. Faux, 22 n'est pas premier.

2. Donner la décomposition en produit de facteurs premiers du nombre 350.
350 =2 x52 x7.
 3. Quel nombre maximal de lots la responsable du magasin pourra-t-elle constituer ?
PGCD(300 ; 350) = 2 x52=50.
4. Dans ce cas, combien y aura-t-il de poissons de chaque type dans chaque lot ?
7 poissons de type A et 6 poissons de type B.
PARTIE B
Le magasin a d’autres poissons, appelés « poissons combattants ».
1. En captivité, il faut prévoir au moins 15 litres d’eau par poisson combattant. Sachant qu’un aquarium est rempli aux 4/ 5 de sa hauteur, lequel doit-on choisir pour un poisson combattant ?
Aquarium 1 : cylindre de 30 cm de diamètre et de hauteur 25 cm.
Volume 3,14 x152 x25x4 / 5=14 137 cm3 =14,1dm3 = 14,1 litres.
Aquarium 2 . pavé droit  : longueur =28 cm , largeur = 28 cm ; hauteur = 30 cm.
Volume : 28 *28 *30 *4/5=18 816 cm3 = 18,8 dm3 = 18,8 litres.
L'aquarium 2 est retenu.
2. Le prix d’un poisson combattant est de 15 €. Une famille achète un poisson combattant et un aquarium. L’aquarium coûte 40 €. Le vendeur propose une remise de 15% sur le prix total. Combien va payer la famille ?
15 +40 = 55 €.
Remise : 55 *0,15 =8,25 €.
prix payé : 55-8,25 =46,75 €.



  
menu