Mathématiques. DNB Centres étrangers 2025.

Partie 1 QCM (20 points)
1. La décomposition en produit de facteurs premiers de 120 est :
120 = 2³ x3 x5 Réponse C.

2. Dans la cellule A2, la formule « = − 4 * A1 - 12 » a été saisie. On l’étire jusqu’à la cellule B2.

	A	B
1	2	5
2	-20

La valeur obtenue dans la cellule B2 est . :
-4 *5-12= -32. Réponse A.

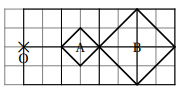
3. Sur la figure ci-dessous, le rapport de l’homothétie de centre O qui transforme le carré A en le carré B est 2.
Réponse D.

4. Une écriture factorisée de 4x² −1 est :(2x-1)(2x+1). Réponse A.

5. Dans le triangle TER ci-dessous, la mesure de la longueur RE arrondie au centième de cm est :

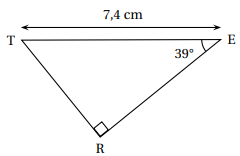
cos 39 = ER / ET ; ER =ET cos 39 =7,4 cos 39=5,75 cm. Réponse B.

Exercice 2. 19 points.
L’entreprise « Transport Rapide » doit livrer cinq colis nommés A, B, C, D et E ayant des masses différentes précisées dans le tableau ci-dessous :

nom du colis	A	B	C	D	E
Masse en kg	4	9	2	7	11

1. Calculer la moyenne des masses des colis en kg.
(4+9+2+7+11) / 5 =6,6 kg.
2. Déterminer la médiane des masses des colis en kg. Interpréter ce résultat.
2 ; 4 ; 7 ; 9 ; 11.
Médiane = 7 kg.
La moitié des colis ont une masse inférieure à 7kg ; l'autre moitié a une masse supérieure à 7 kg.
3. Le transporteur choisit au hasard un colis parmi les cinq (A, B, C, D ou E) pour une livraison express. Calculer la probabilité pour qu’il sélectionne un colis dont la masse est inférieure à 8 kg.
3 cas favorables sur 5 possibles : 3 / 5 = 0,6.
Les colis ont la forme d’un pavé droit de longueur L, de largeur l et de hauteur h, représenté ci-dessous.

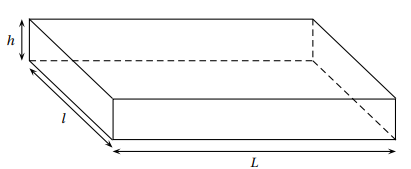4.a Vérifier que le volume du colis E est de 0,12 m³ .
Longueur = 0,5 m ; largeur = 0,4 m ; hauteur =0,6 m.
Volume = 0,5 x0,4 x0,6 =0,12 m³ .
b. L’entreprise souhaite calculer la masse volumique d’un colis. Montrer que la masse volumique du colis E arrondie au dixième est 91,7 kg/m³ .
masse (kg) / volume (m³) =11 / 0,12 = 91,7 kg/m³ .
c. c. Le transporteur affirme « Le colis E est plus lourd que le colis C, donc la masse volumique du colis E est plus grande que celle du colis C ». A-t-il raison ?
Volume du colis C = longueur x largeur fois hauteur = 0,3 * 0,1 *0,5 =0,015 m³.
Masse du colis C = 2 kg..
La masse volumique du colis C est 2 / 0,015 = 133 kg m^-3.
Il n'a pas raison.

Exercice 3. 21 points.
On considère le programme de calcul suivant :
Choisir un nombre
Multiplier le nombre choisi par −2
Ajouter 4 au résultat
Multiplier le résultat obtenu par 4
1. Montrer que si l’on choisit 1 comme nombre de départ dans le programme, le résultat obtenu est 8.
1 *(-2) = -2.
-2+4=2.
2*4 =8.
2. Quel est le résultat si le nombre de départ est −2 ?
-2*(-2) = 4.
4+4=8.
8*4=32.
3. Si l’on note x le nombre de départ, montrer que le résultat peut s’écrire −8x +16.
-2x ; -2x+4 ; (-2x+4) *4 = -8x+16.
4. a. Résoudre l’équation −8x +16 = 4.
16-4=8x ; 12 = 8x ; x = 12 /8 = 1,5.
b. En déduire le nombre de départ qu’il faut choisir pour obtenir 4 comme résultat.
Il faut choisir 1,5.
5. Parmi les trois représentations graphiques ci-dessous, quelle est celle qui représente la fonction f définie par f (x) = −8x +16 ? Expliquer la démarche.

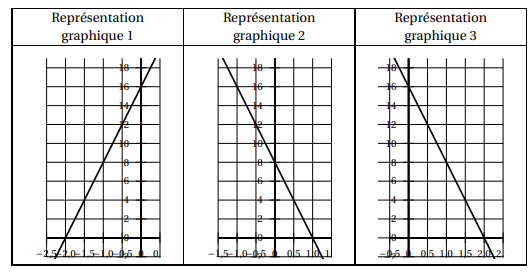
f(0) = 16. Le graphe 2 ne convient pas.
f(2) =-8*2+16=0. Le graphe 3 convient.