Exercice 1 20 points.
On dispose d’une urne A contenant 6 boules numérotées : 7; 10; 12; 15; 24; 30
et d’une urne B contenant 9 boules numérotées : 2; 5; 6; 8; 17; 18; 21; 22; 25.
Les boules sont indiscernables au toucher.
1. On tire une boule dans l’urne A, quelle est la probabilité d’obtenir un nombre pair ?
4 cas favorables (10, 12, 24, 30) sur 6 posibilités : 4 /6 = 2 / 3.
2. On tire une boule dans l’urne B, justifier que la probabilité d’obtenir un nombre premier est de 1/3
3 cas favorables ( 2 ; 5 ; 17 ) sur 9 possibilités : 3 / 9 = 1 /3.
3. Quelle urne contient le plus grand nombre de boules dont le numéro est un multiple
de 6 ?
A : 12 ; 24 ; 30.
B : 6 ; 18.
L'urne A contient le plus grand nombre de boules dont le numéro est un multiple de 6.
4. On tire une
boule au hasard dans l’une des urnes. Démontrer que la probabilité
d’obtenir un nombre supérieur ou égal à 20 est la même quelle que soit
l’urne choisie.
A : 24 et 30. Soit 2 possibiltés sur 6 : 2 /6 = 1 /3.
B : 21, 22, 25.
Soit 3 possibiltés sur 9 : 3 /9 = 1 /3.
5. En repartant avec la composition initiale des urnes A et B on décide d’ajouter une
boule numérotée 50 dans chacune d’entre elles. Dans ces conditions, la probabilité
d’obtenir un résultat supérieur ou égal à 20 est-t-elle toujours égale quelle que soit
l’urne choisie ?
A : 24, 30 et 50. Soit 3 possibiltés sur 7 : 3 / 7.
B : 21, 22, 25 et 50. Soit 4 possibiltés sur 10 : 4 /10 = 2 /5.
Les probabilités sont différentes.
Exercice 2. 23
points.
Cette année, les professeurs d’EPS proposent aux élèves un aquathlon (course à pied et natation).
Partie A : La course à pied
Le parcours de la course à pied est représenté par le dessin ci-dessous (le dessin n’est pas à
l’échelle) :
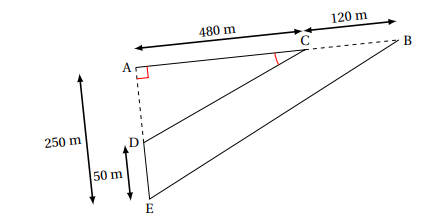
Le parcours est représenté par ACDEB avec le départ au point A et l’arrivée au point B.
Les points A, C, B sont alignés.
Les points A, D, E sont alignés.
ADC est un triangle rectangle en A.
AC = 480 m CB = 120 m
AE = 250 m DE = 50 m.
 1.
1. Justifier que AD = 200 m.
AD = AE-DE = 250-50 = 200 m.
2. Calculer la longueur CD.
Relation de Pythagore : CD
2 = AC
2+AD
2 = 480
2 +200
2 =270 400 : CD = 520 m.
3. Pour que le parcours soit validé il est nécessaire que les droites (CD) et (BE) soient
parallèles et que la mesure de l’angle ACD soit supérieure à 20°.
a. Les droites (CD) et (BE) sont-elles parallèles ?
AD / AE = 200 / 250 = 0,8.
AC / AB = 480 / 600 =0,8.
AD / AE = AC / AB : d'après la réciproque du théorème de Thalès, les droites (CD) et (BE) sont parallèles .
b. La mesure de l’angle ACD est-elle supérieure à 20° ?
tan (ACD) = AD / AC = 200 /480 =0,417.
L’angle ACD mesure 22,6°.
c. Le parcours est-il validé ?
Le parcours est donc validé.
Partie B : La natation.
Concernant l’épreuve de natation, il s’agit de nager une distance de 200 m.
Voici les temps de 9 élèves : 5 min 30 s; 5 min 45 s; 5 min 49 s; 5 min 50 s; 6 min; 6 min 11 s;
6 min 12 s; 6 min 20 s; 6 min 40.
4. Quel est le temps médian de cette série ?
Ranger les temps par ordre croissant :
5 min 30 ; 5 min 30 ; 5 min 45 ; 5 min 49 ; 5 min 50 ;
6 min 11 s;
6 min 12 s; 6 min 20 s; 6 min 40.
Temps médian : 5 min 50.
5. Un poisson rouge nage à la vitesse de 5km/h.
Nage-t-il plus vite que l’élève le plus rapide ?
5 min 30 = 5 *60+30 =330 s.
200 / 330 =0,606 m/s ou 0,606 x3,6 =2,18 km / h.
Le poisson nage plus vite que l'élève le plus rapide.
Exercice 3 QCM. 18
points.
Question 1
Le prix de 3 melons est 8,40 €. Combien coûtent 5 melons ?
8,40 / 3 x5 = 14 € .
Réponse C.
Question 2
Quelle transformation permet de passer de la
figure 1 à la figure 2 ?
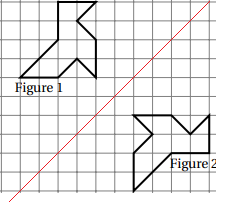
Symétrie autour de la droite rouge.
Réponse D.
Question 3
Un article coûte 350 €. Son prix augmente de 20%. Quel est son nouveau prix ?
350 x1,2 = 420 €.
Réponse A.
Question 4
Quelle est l’aire du triangle rectangle ABC ?
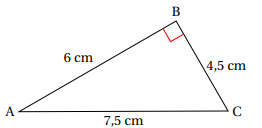
AB x BC /2 = 6 x 4,5 / 2 = 13,5 cm
2.
Réponse B .
Question 5
Quelle est la forme développée et réduite de l’expression (2x +3)(x −4) ?
2x
2-8x+3x-12 =
2x2-5x-12 . Réponse A.
Question 6
Quel est le volume de cette pyramide à base rectangulaire ?
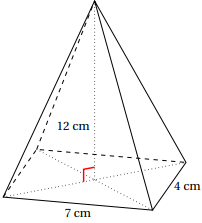
Aire de la base x hauteur / 3 = 4 x7 x12 / 3 =112 cm
3.
Réponse B.