Mathématiques.
DNB Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. 20 points.
Situation 1.
Dans une urne de 40 boules indiscernables au toucher, 5 sont rouges, 20
sont vertes et 15 sont blanches. L’expérience consiste à tirer au
hasard une boule de l’urne et à noter sa couleur.
Calculer la probabilité d’obtenir une boule verte.
Nombre de boules vertes : 20.
Nombre de boules : 40.
Probabilité de tirer une boule verte : 20 /40 = 0,5.
Situation 2
Décomposer en produit de facteurs premiers le nombre 1050. Aucune justification n’est attendue.
1050 =2 x 3 x 52 x7.
Situation 3
Un article coûte 25 €. Calculer son prix après une augmentation de 14 %.
25 x1,14=28,5 €.
Situation 4
Le polygone 2 est un agrandissement du polygone 1.
Le coefficient de cet agrandissement est 2,5.
L’aire du polygone 1 est égale à 7,5 cm².
Calculer l’aire du polygone 2.
7,5 x 2,52=46,875 cm2.
Situation 5
Dans une classe de 3e on note la répartition des tailles des élèves dans le tableau suivant :
Taille (cm)
|
152
|
157
|
160
|
162
|
165
|
170
|
174
|
180
|
Effectif
|
2
|
4
|
2
|
5
|
2
|
4
|
6
|
5
|
a) Quelle est la moyenne des tailles des élèves de cette classe ?
(152 x2 +157 x4 +160 x2 +162 x5 +165 x2 +170 x 4 +174 x6 +180 x5) / (2+4+2+5+2+4+6+5)=5016 / 30=167,2 cm.
b) Quelle est la médiane des tailles des élèves de cette classe ?
La médiane est la moyenne de la 15ème et 16éme taille.
La 15ème taille vaut 165 cm et la 16ème vaut 170 cm.
Médiane = (165+170) / 2 = 167,5 cm.
Exercice 2. 20 points.
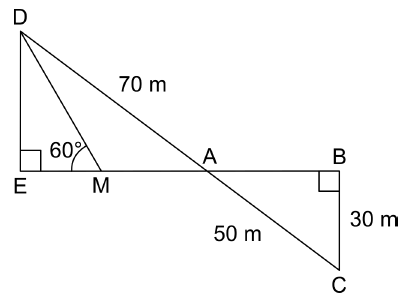
1) Calculer la longueur AB.
Théorème de Pythagore dans le triangle rectangle ABC : AB2 +302=502.
AB2 =502 -302=1600 ; aB = 40 m.
2) Montrer que les droites (DE) et (BC) sont parallèles.
Les droites (DE) et (BC) sont perpendiculaires à la droite (BE) : elle sont donc parallèles.
3) Montrer que la longueur DE est égale à 42 m.
Théorème de Thalès : DE / BC = AD / AC = EA / AB.
DE / 30 = 70 / 50 =1,4.
DE = 1,4 x30 = 42 m.
4) Montrer que la longueur EM est environ égale à 24,2 m.
tan 60 = DE / EM ; EM = DE / tan 60 =42 / 1,732 ~24,2 m.
5) En déduire l’aire du triangle AMD.
Théorème de Thalès : DE / BC = AD / AC = EA / AB.
70 /50 = EA / 40 ; EA = 40 x7 / 5 =56 m.
Aire du triangle ADE : DE x AE / 2 =42 x 56 / 2=1176 m2.
Aire du triangle MDE : DE x ME / 2 =42 x 24,2 / 2=508,2 m2.
Aire du triangle AMD : 1176-508,2 =667,8 m2.
Exercice 3. 20 points.
On considère les deux programmes de calcul suivants :
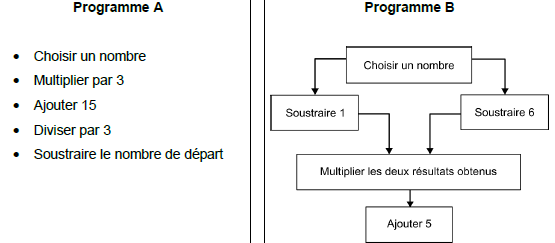
1) Montrer que, lorsque le nombre choisi est 4, le résultat obtenu avec le programme A est 5.
a x3 =12 ; 12+15=27 ; 27 /3=9 ; 9-4=5.
2) Montrer que, lorsque le nombre choisi est – 2, le résultat obtenu avec le programme A est 5.
-2 x3 =-6 ; -6+15=9 ; 9/3 =3 ; 3---2)=5.
3) Justifier que l’affirmation suivante est vraie :
« Le programme A donne toujours le même résultat. »
Soit n le nombre de départ :
(3n+15)/3-n=n+5-n = 5.
4) Lorsque le nombre choisi est 10, quel résultat obtient-on avec le programme B ?
10-1=9 ; 10-6 =4 ;
9 x4=36 ; 36+5=41.
5) Il existe exactement deux nombres pour lesquels les programmes A et B fournissent à chaque fois des résultats identiques.
Quels sont ces deux nombres ?
Soit n le nombre choisi :
le programme A donne 5.
Le programme B donne : (n-1)(n-6)+5=5.
n-1 =0 soit n = 1 ; n-6 = 0 soit n = 6.
|
...
|
....
|
Exercice 4 (20 points)
À l’approche d’une course organisée par son collège, Malo s’entraîne sur un parcours de 13,5 km.
La courbe ci-dessous représente la distance parcourue par Malo (en kilomètres) en fonction du temps écoulé (en minutes).
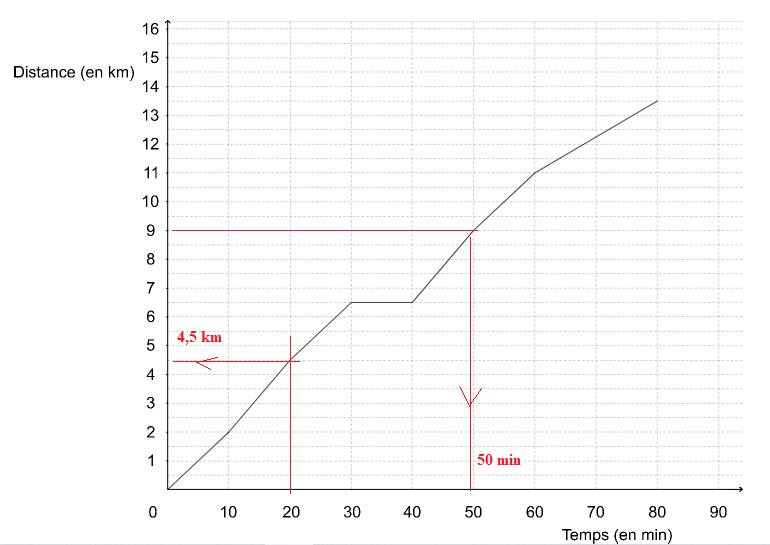
1) Le temps et la distance parcourue par Malo sont-ils proportionnels ?
Non, la courbe n'est pas une droite passant par l'origine.
2) Quelle distance Malo a-t-il parcourue au bout de 20 minutes ?
4,5 km.
3) Combien de temps a-t-il mis pour faire les 9 premiers kilomètres ?
50 min
4) Quelle est la vitesse moyenne de Malo lors de cette course ? Exprimer le résultat au dixième de km/h près.
13,5 / 80 =0,16875 km / min ou 0,16875 x60 ~10,1 km / h.
5) Louise et Hillal
ont couru sur le même parcours de 13,5 km. Louise à une vitesse
régulière égale à 12 km/h et Hillal a une vitesse régulière égale à 10
km/h.
a. Sachant que Louise et Hillal sont partis en même temps, qui a été le premier à franchir la ligne d’arrivée ?
Louise a une vitesse supérieure à celle de Hillal : elle arrive en premier.
b. Quelle distance sépare Louise et Hillal, lorsque le premier des deux franchit la ligne d’arrivée ?
Durée du parcours de Louise : 13,5 / 12 =1,125 heure.
Distance parcourue par Hillal en 1,125 h : 10 x1,125 = 11,25 km.
13,5-11,25=2,25 km.
Exercice 5 (20 points)
Dans cet exercice, aucune justification n’est attendue.
Partie 1 : les motifs.
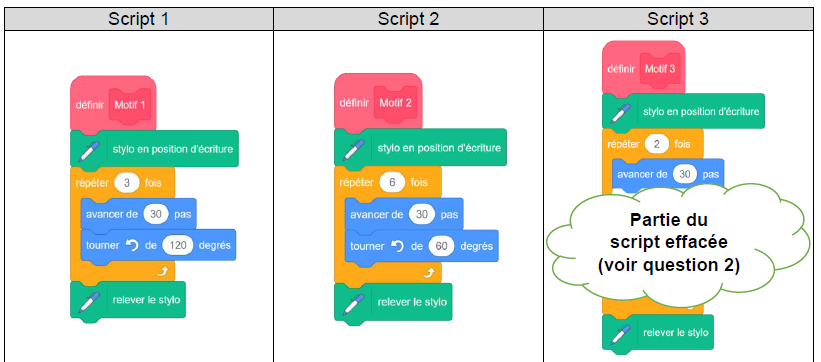
1) Les scripts 1 et 2 permettent chacun d’obtenir un des dessins ci-dessous. Associer chacun des scripts à son dessin.
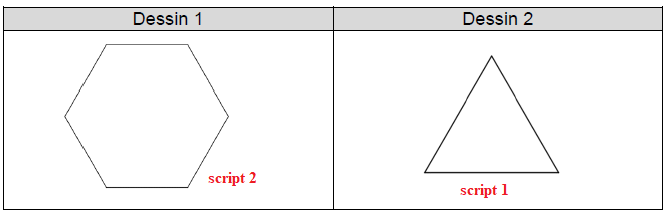
Script 1 : on se déplace 3 fois de 30 pas.
2) Le script 3
permet d’obtenir le losange ci-dessous. La partie du script effacée
contient les 3 instructions A, B et C ci-dessous.
Sur votre copie, recopier dans le bon ordre les instructions cachées.
Chaque instruction ne doit être utilisée qu’une seule fois.
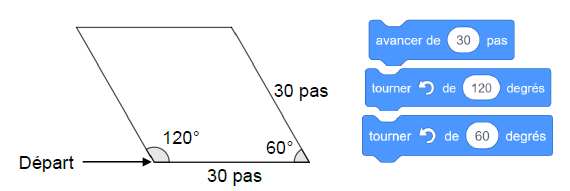
Partie 2 : le script principal.
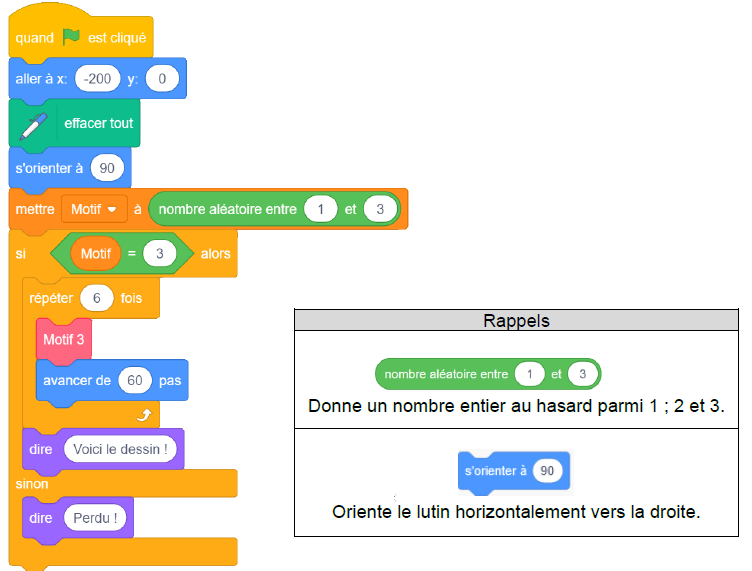
3) Quelles sont les coordonnées du point de départ du lutin ?
-200 ; 0.
4) Parmi les 5 captures d’écran proposées ci-dessous, seules deux sont possibles. Lesquelles ?
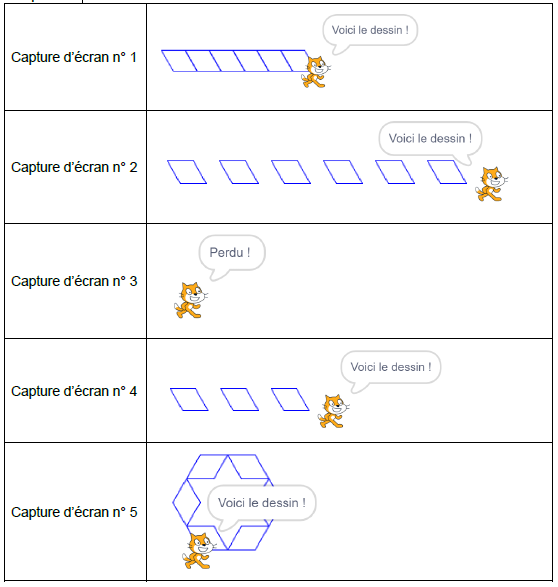
On peut obtenir les captures d'écran 2 et 3.
5) On clique sur le
drapeau vert, et on observe le message affiché. Quelle est la
probabilité que le message affiché soit « Voici le dessin ! » ?
La probabilité de tirer 3 et 1 /3.
La probabilité que le message affiché soit « Voici le dessin ! » est 1 /3.
6) On lance de nouveau le programme 100 fois et on regroupe les résultats obtenus dans le tableau suivant :
Message du lution
|
Voici le dessin !
|
Perdu !
|
Effectif
|
40
|
60
|
a) Calculer la fréquence de l’affichage « Voici le dessin ! ».
40 /100 = 0,4.
b) Pourquoi ce résultat est-il différent de celui obtenu à la question 5 ?
Il faudrait exécuter une infinité de fois le programme pour que la fréquence soit égale à la probabilité.
|
|
|
|