Mathématiques.
Concours
technicien de la police
technique et scientifique. Zone ouest 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Mathématiques. 40 points.
Q1.
Exprimer a = ln(24) en fonction de ln(2) et ln(3).
ln(24) = ln(8 x3) = ln(23x3) =ln(23)+ln(3) = 3
ln(2) + ln(3). Réponse A.
Q2. Ecrire B = ½ln(9) -2 ln(3) sous
la forme d'un seul logarithme.
B = ln(9½) -ln(32) =ln(3) -ln(9) = ln(3 / 9) =
ln(1/3). Réponse D.
Q3.
La comparaison de x = ln(5)-ln(2) et y = ln(12)-ln(5) donne :
x = ln(5/2) = ln(2,5) ; y = ln(12/5) = ln(2,4). x >y. Réponse B.
Q4.
L'équation ln(|x|3+2)=ln(2x2+|x|
apour ensemble de solutions :
si x = -0,5 : ln(0,125+2) = ln(2,125) ; ln (2x0,25+0,5)=ln(1)=0.
si x = -3 : ln(27+2) = ln(29) ; ln
(2x9+3)=ln(21).
si x = 3 : ln(27+2) = ln(29) ;ln(18+3) = ln(21).
si x = -2 : ln(8+2)= ln(10) ;
ln(2*4+2)=ln(10).
si x = -1 : ln(1+2)= ln(2+1)
si x = 1
: ln(1+2)= ln(2+1)
si x = 2
: ln(8+2)= ln(8+2). Réponse B.
Q5 .L'ensemble de
définition de la fonction f(x) = ln((4-x2) / x) est :
(4-x2) / x >0 avec x différent de zéro et différent de ±2.
(2-x)(2+x) / x >0.
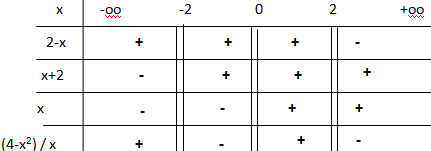
Réponse C.
Q6. Le sens de
variation de la fonction g définie sur ]0 ; +oo[ par g(x) =x2-2ln(x)
est :
g'(x) = 2x-2/x =(2x2-2) / x = 2(x2-1)/x.
Si x appartient à ]0 ; +1[, g'(x) >0 et g(x) est strictement
croissante.
Si x appartient à ] 1 ; +oo[,
g'(x) < 0 et g(x) est strictement décroissante.
Si x =1, g'(x)=0 et g(x) présente un maximum. Réponse D.
Q7. Une primitive de f(x) = x2-5x+1/x
sur ]0 ; +oo [ est :
F(x) = x3/3-5x2/2+ln(x). Réponse C.
Q8 La suite (un) de réels
strictement positifs, définie par u0 = 2 et ln(un+1)
= 1 +ln(un) . On a :
ln(un+1)-ln(un) = 1 = ln(e) ; ln(un+1/un)
= ln(e) ; un+1/un
= e : un+1 = e un.
Suite géométrique de premier terme 2 et de raison e. Réponse A.
Q9. La valeur de l'intégrale
suivante est :
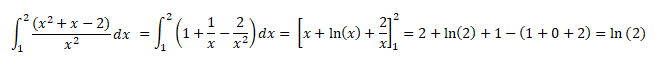
Réponse C.
Q10.
Le temps T mis par le crocodile pour rejoindre sa proie peut être
minimisé s'il nage jusqu'à un point particulier P.
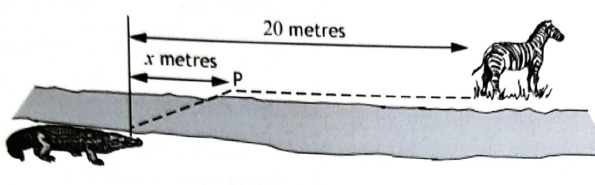
T(x) = 5 (36+x2)½
+4(20-x).
La valeur de x qui minimise ce temps est :
On dérive : T ' (x)=5*0,5 *2x *(36+x2)-½
-4 =5x
(36+x2)-½
-4.
La dérivée s'annule si : 5x(36+x2)-½
=4 ; 5x
= 4(36+x2)½.
25x2 =16(36+x2
); 25x2 =36*16 +16x2 ; 9 x2 =36 x16 ; x2
=4 *16 ; x = 8. Réponse A.
Q11. h(x) = 0,5 p exp(-½x2). Sa
dérivée est :
h'(x) =0,5
p (-x)
exp(-½x2).Réponse A.
Q12. Les limites de
f(x) = (4e2x+1) / (ex(2ex+1)) en +oo
sont :
f(x) = (4e2x+1)
/ (2e2x+ex).
Mettre e2x en facteur et simplifier : f(x) = (4 +e-2x)
/(2+e-x).
En +oo, e-2x et e-x tendent vers zéro : f(x) tend
vers 2. Réponse C.
Q13. Soit f une
fonction définie sur R et telle que 1 < f(x) < 2.
La limite de f(x) / x quand x tend vers +oo est :
1
/ x < f(x)
/x < 2 / x.
En +oo, f(x) / x tend vers zéro. Réponse
A.
Q14. La solution de
l'équation 2e-x = 1 /(ex+1) est :
2(1+e-x)=1 ; 1+e-x=
0,5 ; e-x = -0,5 ; ex = -2 ; or ex
>0, pas de solution. Réponse D.
Q15.
La fonction f2 est continue et strictement décroissante sur
]0 ; +oo[.
La
fonction f1 est continue et strictement croissante sur ]0 ;
+oo[.
La limite en +oo de la fonction f1(x) est +oo.
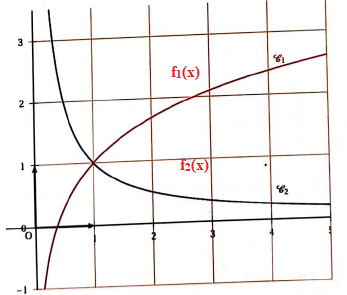
La limite quand x tend vers +oo de f2(x) est 0 ; l'axe des
abscisses est asymptote. Réponse A.
Q16. Les montants
réalisés à l'exportation des perles est modélisé par une suite (un).
En 2014 le montant en milliers d'euros est noté u0 =61 182.
Le montant en 2011+n est noté un.
La valeur baisse tous les ans de 8 %.
En 2012 : u2011=A ; u2012 =0,92 A ;
en 2013 : u2013=0,922 A ; en 2014 : u2014
= 0,923A = 61 182.
A = 78 570.
La suite est géométrique de raison 0,92 et de premier terme u0=78
570. Réponse A.
Q17. D'après la
question précédente, le montant cumulés des produits perlés entre 2011
et 2020 est :
n = 2020-2011 = 9.
Somme des 9 premiers termes de cette suite géométrique : 78 570 x 0,9210
/(1-0,92 )=426 624 €. Réponse B.
Q18. Un
laboratoire a réalisé des tests sur 800 patients atteints d'une
maladie.
|
Médicament
A
|
Médicament
B
|
Total
|
Guéri
|
383
|
291
|
674
|
Non
guéri
|
72
|
54
|
126
|
Total
|
455
|
345
|
800
|
On
choisit un patient au hasard et on considère les événements :
A : prise du médicament A ; G : pateint guéri.
On choisit au hasard un patient guéri. La probabilité qu'il est pris le
médicament A est :
383 / 674 =0,57. Réponse B.
Q19. On souhaite
mesurer l'effet d'un médicament sur la migraine. On constitue deux
groupes de 100 personnes.
Le groupe A reçoit le médicament et le groupe B un placebo.
Groupe A : 68 % ont vu leur migraine diminuer.
Groupe B : 56 % ont vu leur migraine diminuer.
A l'aide d'intervalle de confiance au seuil de 95 %, que peut-on
conclure ?
A
: 1,96 ( p(1-p) / n)½ =1,96
x(0,68 x 0,32 )½/ 10 =0,091. [0,68-0,091 ; 0,68+0,091 ) soit
[0,55 ; 0,77].
B
: 1,96
x(0,56 x 0,44)½ / 10 =0,098. [0,56-0,098 ; 0,56+0,098 ) soit
[0,46 ; 0,66].
Les intervalles ne sont pas disjoints : on ne peut pas conclure. Réponse C.
Q20. On capture 200
poissons d'un lac que l'on marque puis qu'on relache. Quelques jours
plus tard on capture 500 poissons, l'un après l'autre que l'on relâche
immédiatement. Parmi les 500 poissons, 220 étaient marqués. Un
encadrement du nombre total de poissons dans le lac avec un niveau de
confiance de 95 % est de :
Fréquence des poissons dans l'échantillon : 220 / 500 =0,44.
Intervalle de confiance : 0,44 -1/500½ ; 0,44 +1 /500½
soit 0,395 ; 0,485.
1/ 0,395 > N /200 > 1/0,485 ; 200 / 0,395 > N > 200 /0,485 ;
506 > N >412. Réponse C.
|
...
|
....
|
Q21.
Une étude a établi qu'un client sur 4 pratique le surf. Dans une
télécabine accueillant 80 clients, quelle est la probabilité qu'il y
ait exactement 20 clients pratiquant le surf.
X : variable aléatoirecomptant le nombre de surfeurs.
S : le client pratique le surf : p(S) = 0,25.
X suit la loi binomiale de paramètre n =800 , p = 0,25.
P(X) = 20 =(80 20) x0,2520 x0,7560
= 0,103. Réponse A.
Q22. l'épaisseur
maximale d'une avalanche ( en cm) est modèlisée par une variable
aléatoire X qui suit la loi normale de moyenne µ =150 cm et d'écart
type inconnu. P(X >
200) =0,025 ; Calculer P(X >
100).
P(X > 200)=P(X > 150+50 )= 0,025.
P(X <
150-50)=0,025. P(X <
100) =0,025.
P(X > 100)
=1-0,025 = 0,975. Réponse D.
Q23. Dans un
couloir neigeux, on modélise l'intervalle de temps séparant deux
avalanches par une variable aléatoire T qui suit une loi exponentielle.
E(T) = 5 ans ; la probabilité P(T > 5) est égale à :
l = 1 /5 = 0,2.
P(T >5) =exp(-0,2
x5) = e-1. Réponse C.
Q24. Chaque jour la
maman de Rose arrive à la maison à 12 h et repart à 12 h 30. Rose
arrive aléatoirement entre 11 h45 et 13 h15 et reste 5 minutes avant de
repartir. Quelle est la probabilité qu'elles se croisent ?
X variable aléatoire qui indique l'instant d'arrivée de Rose en minute
à partir de 11 h45.
13 h15-11h45=90 minutes.
X suit une loi uniforme sur [0 ; 90].
Rose doit arriver entre 11 h55 et 12 h30 pour croiser sa maman.11 h55
-11h45 =10 min ; 12 h30-11h45 = 45 min..
p(10 < X <45)=(45-10) / 90 =35
/90 =7 /18. Réponse A.
Q25. La masse en
grammes d'un melon est schématisée par une variable aléatoire M qui
suit une loi uniforme sur [850 ; x] avec x > 1200.
75% des melons ont une masse comprise entre 900 g et 1200 g. La valeur
de x est alors :
P(900 < X< 1200) = (1200-900) /
(x-850) = 0,75.
300 / (x-850) = 0,75 ; x-850 = 200 / 0,75 = 400. x = 850+400 = 1250. Réponse
D.
Q26. On étudie la
production d'une usine qui fabrique des bonbons conditionnés en
sachets. On choisit au hasard un sachet. Sa masse en gramme est
modélisée par une variable aléatoire X qui suit une loi normale
d'espérance µ=175. De plus 2 % des sachets ont une masse inférieure ou
égale à 170 g, ce qui se traduit par : P(X <170)=0,02.
Quelle est la probabilité de l'événement " la masse du sachet est
comprise entre 171 et 180 g ?
Pour tout nombre positif a : P(X < 175-a)=P(X > 175+a).
Pour a = 5 : P( X <
170.)= P(X >180)=0,02.
P(170 < X < 180)=1-P(X<170)-P(X >180)=1-0,02-0,02=0,96. Réponse B.
Q27. On étudie
l'évolution d'un médicament après son administration dans l'organisme
en mesurant sa concentration plasmatique. On note f(t) cette
concentration en microgramme / L au bout de t heures après
l'administration.
f(t) = 20 exp(-0,1t) ; f(0) = 20 µg / L.
La demivie t0,5 est la durée en heures après laquelle la
concentration plasmatique est égale à la moitié de sa concentration
initiale.
Cette demi-vie est :
10 = 20 exp(-0,1 t0,5) ; 0,5 = exp(-0,1 t0,5) ;
ln(0,5) = -0,1t0,5 ; t0,5 =6,9 h. Réponse A.
Q28. f(x) = 4ex
/ (ex+1). Le sens de variation de cette fonction est :
On dérive en posant u = 4ex et v = ex+1 ;
u' = 4ex ; v' = ex.
(u'v-v'u) / v2 =[4ex(ex+1) -4exex] / (ex+1)2=4ex/ / (ex+1)2 >0.
f(x) est croissante sur R. Réponse A.
Q29. f(x) = ex-1/ex.
La résolution de l'inéquation ex-1 / ex < 0 :
ex < 1/ex
; e2x < 1
; 2x < ln(1) : 2x < 0. Réponse D.
Q30. La limite en
zéro de 4 ln(x+0,5) / x est :
ln(x+0,5) tend vers ln(0,5) = -0,69.
4 ln(x+0,5) / x tend vers moins l'infini. Réponse C.
Q31. Equation
différentielle 2y'-y = 4x+1. La fonction g(x) = ax+b est solution de
cette équation.
g'(x) = a ; repport dans l'équation :
2a-ax-b = 4x+1.
On identifie : a = -4 ; 2a-b = 1 ; b = 2a-1 = -9. Réponse B.
Q32. Donner la
solution générale de l'équation différentielle (E) : y'+2y = -4 ; y(1)
= -3.
Solution générale de y'+2y = 0 : y = A exp(-2t).
Solution particulière de (E) : y = -2.
Solution générale de (E) : y =A exp(-2t)-2.
y(1) = A e-2 -2=-3 ; A = -e2 ; y = -exp(2-2t)-2. Réponse C.
Q33.
Budget
publicitaire en milliers d'euros (xi)
|
8
|
10
|
12
|
14
|
16
|
18
|
Cjffre
d'affaires en milliers d'euros (yi)
|
40
|
55
|
55
|
70
|
75
|
85
|
Soit G1 le point moyen associé aux trois premiers
points et G2 le point moyen associé aux trois derniers.
La droite d'ajustement passe par les points de coordonnées :
G1 (10 ; (55+55+40) /3 ) soit (10 ; 50).
G2(16 ; (70+75+95)/3) soit (16 ; 80). Réponse D.
Q34.
Nombre
de buts (xi)
|
2
|
8
|
11
|
16
|
20
|
Salaire
annuel en millions d'euros (yi)
|
3,5
|
4,7
|
5,2
|
7,6
|
9,5
|
Une équation la
droite d'ajustement est :y = 0,34x +2,26. Réponse A.
Q35. Reprenons
l'énoncé de la question 34. S'il marque 25 buts, son salaire serait :
0,34 x25 +2,26 = 10,76 millions d'euros. Réponse C.
Q36. f(x) = x2+1
; g(x) = -x2+2x+5.
L'aire délimitée par les courbes de f et g sur (-1 ; 2) est alors :
Primitives : F(x) = x3 / 3+x ; G(x) = -x3/3 +x2+5x.
G(x) -F(x) =-2x3/3 +x2+4x.
G(-1)-F(-1) = 2 /3+1-4 = 2 /3 -3.
G(2)-F(2) =-16 /3+4+8 =
-16 /3 +12.
-16 /3+12-(2/3-3)=-18 /3+15=9 ua. Réponse C.
Q37. On modélise le
nombre de malades d'une épidémie par f(x) = 16x2-x3.
Le nombre moyen de malades sur une période de 16 jours est :
F(x) = 16 / 3 x3
-x4 / 4.
F(0) = 0 ; F(16)=164/3 -164/ 4 =164/ 12.
[ F(16) /F(0) ] / 16 = 163/
12 = 16 x16 x16 / 12 = 4 x16x16 / 3=1024 /3. Réponse D.
Q38.
Une solution a une concentration en ion H3O+ de 2
10-11 mol / L.
pH = - log(2 10-11) =10,7. Réponse C.
Q39. g(x) = x-ln(x)
définie sur ]0 ; +oo[.
g'(x) = 1-1/x = (x-1) / x.
g'(x) est négative sur ]0 ; 1[ et g(x) est strictement décroissante sur
cet intervalle.
g'(x) est
positive sur ]1 ; oo[ et g(x) est strictement croissante sur cet
intervalle.
g(x) est décroissante sur ]0
; 1] et g(x) est strictement croissante sur ]1 ; +oo[.
Q40. Soit une somme de 2000 euros
placée à 4 %. La somme obtenue au bout de 10 ans est :
2000 x 0,04 =80 euros d'intérêts par ans soit 800 € d'intérets en 10
ans.
2000 +800 = 2800 . Réponse C.
|
|
|
|