Mathématiques.
Concours
technicien de la police
technique et scientifique. Zone est 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Mathématiques. 20 points.
Q1.
Déterminer les limites des fonctions suivantes.
f(x) = ex/ x quand x tend vers +oo.
Par croissance comparée f(x) tend vers +oo.
. Réponse B.
Q2. f(x) = ln(x) / x quand x tend
vers +oo.
Par croissance comparée f(x) tend vers zéro. Réponse C.
Q3.
f(x) = ln(x) /xn pour n >0 quand n tend vers +oo.
Par croissance comparée f(x) tend vers
zéro. Réponse D.
Q4.
f(x) = x ex quand x tend vers -oo.
ex tend vers zéro et f(x) tend vers zéro. Réponse A.
Q5 .f(x) = xn
quand x tend vers +oo ( n < 0).
f(x) tend vers zéro. Réponse C.
Q6. f(x) = ln(1+x)
/ x quand x tend vers zéro.
ln(1+x) = [ln(x+1) -ln(1)] / x.
c'est [ f(x+a)-f(a)] / x = f '(a) avec a = 1.
f '(1) / 1 = 1 / 1 = 1
. Réponse B.
Q7. f(x) = (ex+1) / x
quand x tend vers zéro.
ex+1 tend vers 2 ; f(x) tend vers +oo. Réponse B.
Q8 f(x) = xn e-x
quand x tend vers +oo ( pour n >0).
f(x) =
xn / ex .
Par
croissance comparée f(x) tend vers zéro. Réponse A.
Déterminer le domaine de de définition des fonctions suivantes :
Q9. (x5-1) / (x2-1).
Le dénominateur ne doit pas être nul soit x différent de 1 et -1.
R-{-1 ; 1}. Réponse D.
Q10.
g(x) = 1 / (x-1)½.
x-1 doit être strictement positif soit x > 1.
Réponse D.
Q11. g(x) = (2-x)½
/ (x2-9).
2-x doit être positif ou nul soit x < 2.
Le dénominateur ne doit pas être nul soit x différent de -3 et +3.
]-oo ; -3 [ union ]-3 ; 2]. Réponse B.
Q12. g(x) =5x3-x2+3x-6.
Ensemble des réels R. Réponse C.
Soit f(x) = ln(x) +ln(x-1)-ln(6).
Q13. Quel est
l'ensemble de définition de cette fonction ?
x -1 >0 soit x > 1.
Réponse B.
Q14. Résoudre
l'équation ln(x)
+ln(x-1)-ln(6)=0.
ln(x(x-1) / 6) =0 = ln(1).
x(x-1) / 6 = 1
x2-x-6=0.
Discriminant : 1+4*6=25 = 52.
Solution retenue : (1+5) / 2 = 3.
Réponse C.
Q15.
Quelle est la dérivée de f(x) ?
f(x)
=ln(x(x-1) / 6)= ln(x2-x) -ln(6)
On pose u = x2-x ; u' = 2x-1.
f '(x) = u' /u =(2x-1) / (x2+x).
h(x) = ln(x)-2+x définie sur ]0 ; +oo[.
Q16. Déterminer ces
limites en zéro.
En zéro, ln(x) tend vers -oo ; -2 +x tend vers 0.
Limite de h(x) en zéro : -oo. Réponse
B.
Q17. Déterminer la
limite de h(x) en +oo.
h(x) = x (ln(x)/x-2/x+1).
Par croissance comparée ln(x) / x tend vers zéro ; 2 /x tend vers zéro.
h(x) tend vers +oo.
Réponse A.
Q18. Calculer la
dérivée h '(x).
h '(x) = 1/x+1.
Réponse B.
Q19. En déduire le
sens de variation de h(x).
h '(x) = (x+1) / x avec x appartenant à ]0 +oo[.
h'(x) >0 et h(x) est strictement croissante.
.
Réponse D.
Q20. 75 % des
clients sont des femmes. Une femme sur 5 achète un article au rayon
bricolage alors que 7 hommes sur 10 le font. Une personne choisie au
hasard a fait un achat au rayon bricolage. La probabilité que cette
personne soit une femme est
Formule des probabilités totales :
P(B)=P(F n B)+P(H n B) = 0,75 x0,2 +0,25 x0,7 = 0,325.
PB(F) = P(B n F)/ P(B) = 0,75 *0,2 / 0,325 = 0,462.
Réponse C.
|
...
|
....
|
Q21.
Un modèle d'ordinateur e st en promotion. La probabilité qu'un clent
achète ce modèle est 0,3. On considère un échantillon de 10 clients qui
sont intéréssés par ce modèle. La probabilité qu'exactement 3 clients
l'achète est :
La variable X qui compte le nombre de clients qui achètent l'ordinateur
suit une loi binimiale de paramètres n = 10 et p = 0,3.
p(X = 3) = (10 3)x0,33 x0,77
= 0,267.
Réponse D.
Q22. G(x) = 3x2e2x
-5 est une primitive de :
On dérive en posant u = 3x2 et v = e2x.
u' = 6x ; v' = 2e2x.
u'v+v'u = 6x e2x +6x2e2x =6x(1+x)e2x.
Réponse A.
Q23. La solution
particulière constante de (E) : y' =2y+5 est :
f(x) = -5 /2 = -2,5. Réponse A.
Q24. (un)
est une suite géométrique de raison b=2 et de premier terme u0=1/8.
Calculer u10.
u1 = b u0 = 1/4 ; u2 = b u1 =2 /4 =22 x
1/8)=1/2 ; ... u10 =u0 b10 =1 / 8 x210
=128.
Réponse B.
Q25. L'équation ln(x2-x)=0
a pour solution :
ln(x2-x) = ln (1) ; x2-x = 1 ; x2-x-1
= 0.
Discriminant : 1+4=5.
Solutions (1±5½) / 2.
. Réponse C.
Q26. Soit g une
fonction dérivable sur R ayant pour tableau de variations :
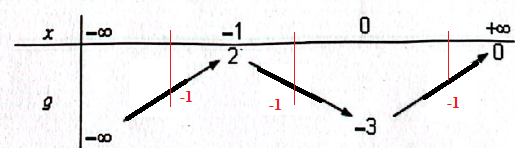
Le nombre de solutions dans R de g(x) = -1 est : 3. Réponse D.
Q27. g'(x) est
négative sur :
g(x) est décroissante sur ]-1 ; 0[.
Réponse C.
|
|
|
|