Filtre
passe bande, série de Fourier. Bts maths groupe A 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une
enceinte acoustique transforme une puissance électrique en pression
acoustique. Elle comporte plusieurs haut-parleurs pour restituer les
plages de fréquences audibles car il n’existe pas de haut-parleur qui
puisse restituer la totalité de ces fréquences.
Exercice
1.
On étudie un des blocs de filtres utilisés. Il est constitué de deux
filtres F1 et F2.
Pour le filtre F1, on note : H1
sa fonction de transfert, G1(w)=
20log |H1(jw)|, w1
la pulsation de coupure à −3 dB du filtre c’est-à-dire la
pulsation w1 pour laquelle le gain en
décibel est égal à −3 (on admet qu’il n’y en a qu’une), f1
la fréquence associée à w1 .
La bande passante du filtre F1 est l’ensemble
des fréquences que le filtre laisse passer. On considère que ce sont
les fréquences associées à un gain en décibel supérieur ou égal à −3.
On adopte les notations et le vocabulaire analogues pour le filtre F2.
Partie
A : cas du filtre F1.
On donne la représentation graphique de la fonction G1.
1.
Déterminer graphiquement une valeur approchée de la pulsation de
coupure w1 du filtre F1.
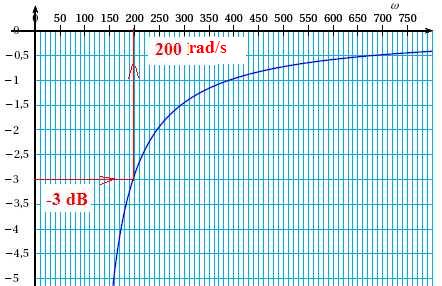
w1
=200 rad/s ;
f1 =200 /(2 p)=31 Hz.
2.
En déduire une estimation au hertz près de la fréquence de
coupure f1 du filtre F1, une estimation de la
bande passante du filtre F1.
Le filtre laisse passer les fréquences supérieures à 31 Hz.
Partie
B : cas du filtre F2.
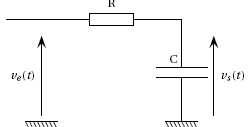
Le filtre F2 est représenté sur le schéma
ci-dessous. Les tensions d’entrée ve et de
sortie vs sont des fonctions causales vérifiant
: ve (0) = 0, vs (0) = 0
et vs (t )+RCv′s (t )= ve
(t ) (1).
On note Ve et Vs les
transformées de Laplace de ve et vs
.
1. La fonction de
transfert H2 du filtre F2
vérifie, pour tout réel p strictement positif :
H2(p) = Vs (p) / Ve
(p).
En appliquant la transformation de Laplace aux deux membres de
l’égalité (1), démontrer que
H2(p)= 1 / (1+RCp ).
(1) s'écrit : Vs(p)
+RCp Vs(p) = Ve(p).
Vs(p) (1+RCp) =
Ve(p) ; Vs(p) /
Ve(p) = 1
/ (1+RCp ).
2. On souhaite
connaître la tension de sortie vs qui est
obtenue lorsque la tension d’entrée ve est un
échelon d’amplitude 5V , autrement dit lorsque pour tout réel t :
ve (t ) = 5 U(t ) avec U(t )= 0 si t
< 0 et 1 si t >0.
a.
Donner Ve (p) puis calculer Vs
(p) en fonction de R, C et p.
Ve (p) =
5 / p ; Vs (p) = Ve
(p) / (1+RCp) = 5 / [p (1+RCp) ].
b. Démontrer que : Vs
(p)=5 /p -5 / [ p+1/(RC)].
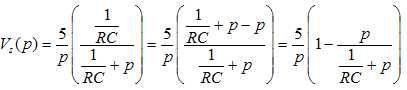 c. En déduire vs
(t ) pour tout réel positif ou nul.
c. En déduire vs
(t ) pour tout réel positif ou nul.
vs(t) = 5 (1-e [-t/ (RC)]).
a. Calculer le module |H2(jw)|
du nombre complexe H2(jw).
H2(jw)
= (1 -RCjw
) / [1+(RCw)2].
|H2(jw)|
= 1 /
[1+(RCw)2]½.
b. En déduire que : G2(w) =
−10 / ln(10) ln
[1+(RCw)2]
G2(w) =
20 log |H2(jw)|
= 20 / ln10 ln {1
/
[1+(RCw)2]½}
G2(w) =
-10 / ln10 ln[1+(RCw)2].
|
| .
. |
|
|
4. Étude de la
fonction G2.
a.
Montrer que pour tout réel positif w : G′
(w) = 1/ ln10 (-20(RC)2w /
[1+(RCw)2].
On pose u = 1+(RCw)2
; u' = 2 (RC)2w.
G′
(w) = -10 /
ln(10) 2
RCw / [1+(RCw)2] = -20(RC)2w / [1+(RCw)2].
b. En déduire les
variations de la fonction G2 sur l’intervalle [0
; +oo[.
G′ (w) est négative sur l'intervalle
[0 ; +oo[. G2 est décroissante.
c. Déterminer
la limite de G2(w)
quand w
tend vers l'infini.
[1+(RCw)2est
équivalent à +(RCw)2
et
ln[(RCw)2tend
vers l'infini si w
devient grand.
G2(w)
tend vers moins l'infini quand w devient
grand.
d. Dresser le
tableau de variations complet de la fonction G2 sur l’intervalle [0 ;
+oo[.
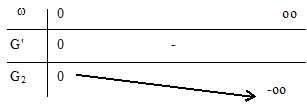
5.
Détermination de la bande passante du filtre F2.
a.
Calculer G2 [1/(RC) ]. RCw = 1.
G2 [1/(RC) ] = -10 / ln10 ln[1+1]
=
-10 / ln10 ln2 = -3 dB.
En conséquence, la fréquence de coupure de ce filtre est w2
= 1 / (RC).
b. Pour la suite de
l’exercice on prend : R = 160×103 W et C
= 3,4×10−9 F.
Donner une valeur approchée arrondie à l’unité de la fréquence de
coupure f2.
w2
=
1/ (160 103 *3,4 10-9)
=1,84 103 rad/s ; f2 =w2
/(2p)=292,7
~293 Hz.
c. Quelle est la
bande passante du filtre F2 ? Justifier.
La bande passante du filtre est l’ensemble des fréquences que
le filtre laisse passer. On considère que cesont les fréquences
associées à un gain en décibel supérieur ou égal à −3.
Bande passante [0 ; 293Hz ].
Le bloc de filtres étudié dans l’exercice est constitué des filtres F1
et F2.
La bande passante de ce bloc de filtres est l’ensemble des fréquences
que le filtre F1 et le filtre F2
laissent tous les deux passer.
1.
Quelle est la bande passante du bloc de filtres étudié ?
[31 ; 293 Hz ]
2.
Auquel des trois haut-parleurs de l’enceinte acoustique est associé le
bloc de filtres étudié ?
Basses fréquences, sons graves ( boomer).
|
|
|
|
Exercice 2.
On considère un signal modélisé par une fonction s, paire et périodique de période T = 2, vérifiant :
s(t ) = 2t si 0<=t<=0,5 et s(t ) = 1 si 0,5<t<=1.
Partie A : série de Fourier associée à la fonction s.
On admet que la fonction s est développable en série de Fourier.
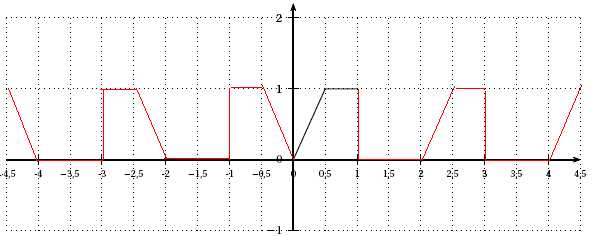
Compléter la représentation graphique de la fonction s sur l’intervalle [−4 ; 4].
La fonction étant paire, le graphe est symétrique par rapport à l'axe vertical.
2. Établir que : a0 =0,75.
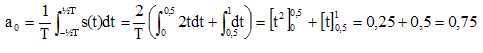
3. Préciser la valeur de bn pour tout entier naturel n non nul. Justifier.
La fonction étant paire, les coefficients bn sont nuls.
4. On veut calculer an.
Démontrer alors que pour tout entier non nul n :
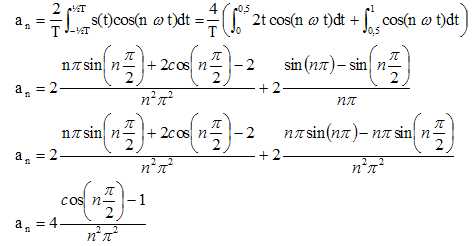
5. Recopier et compléter le tableau ci-dessous. On y portera les valeurs approchées à 10−3 près de an pour n compris entre 1 et 7.
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| an |
-0,405 |
-0,203 |
-0,045 |
0 |
-0,0162 |
-0,0225 |
-0,00827 |
.
|
ans
|
|
Partie B : puissance du signal
1. La fonction s étant paire, la puissance du signal sur une période T est donnée par :
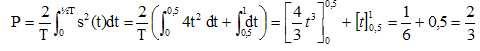
2. On rappelle la formule de Parseval :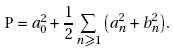
On considère l’algorithme :
n entier naturel, S nombre réel, a nombre réel
n prend la valeur 0
S prend la valeur 0,752
Tant que S <99,9 / 100 × 2/3
faire
n prend la valeur n +1
a prend la valeur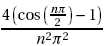
S prend la valeur S +½a2
Fin tant que
Afficher n
a. Quelle valeur de n affiche l’algorithme ? Justifier.
n
|
0
|
1
|
2
|
3
|
S
|
0,5625
|
0,64463
|
0,66516
|
0,6662
|
b. Que représente cette valeur pour le signal étudié ?
Pour n =3, 99,9 % de la puissance totale du signal est atteinte.
|
|