Série
de Fourier, transformée de Laplace. Bts maths groupe A 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1. Partie
A.
On considère la fonction f , périodique de période T , dont une
représentation graphique est donnée par la figure ci-dessous.
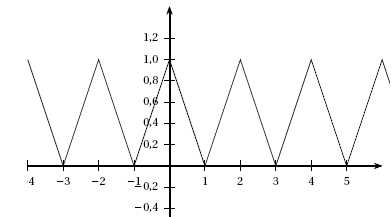
Le développement en série de Fourier de la fonction f est noté :
a0 + S (an
cos (npt)
+bn sin(npt)
1.
Cette question est un QCM.
Pour
chaque affirmation, une seule des propositions est exacte. Le candidat
portera sur la copie, sans justification, le numéro de la question
suivi de la réponse choisie.
a.
La période T de la fonction f est :0,5 ; 1 ; 2 ( vrai ) ; 3.
b.
Le coefficient b1 vaut : -4 / p2
; 0 (vrai)
; 0,25.
La fonction f est paire ( symétrie par rapport à l'axe des y) , les
coefficients bn sont nuls.
c.
Le nombre réel a0 vaut : 0 ; 0,25 ; 0,5 (vrai)
; 12.
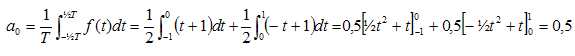
d.
On donne l’égalité suivante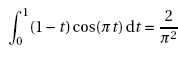
La valeur exacte du coefficient a1 est :0 ; 4 /p2 (vrai); 2 /p2 ; 1 /p2 .
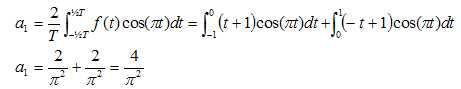
Application de la
formule de Bessel-Parseval.
2.
On rappelle que la puissance moyenne Pf , par
période du signal, modélisé par une fonction f de
période T est donnée par la relation suivante. Démontrer que Pf
=1/3.
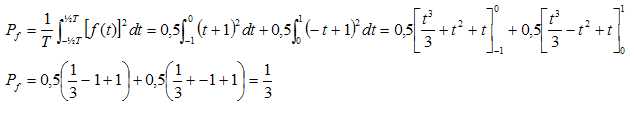
3.
On note gn la fonction définie, pour tout nombre
entier n strictement positif par :
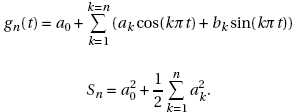
Compléter le tableau.
| n |
1 |
2 |
3 |
4 |
5 |
6 |
| a2n |
0,1643 |
0 |
0,0020 |
0 |
0,0003 |
0 |
| Sn |
0,3321 |
0,3321 |
0,3321
+0,5 *0,0020
=0,3331 |
0,3331 |
0,3331
+0,5 *0,0003
=0,3333 |
0,3333 |
b. En déduire la
plus petite valeur de l’entier n telle que la puissance moyenne par
période de la
fonction gn est supérieure ou égale à 0,999Pf
.
0,999Pf
=0,999*1/3 =0,333 ; donc n
= 3.
|
| .
. |
|
|
Partie B.
Soit t
un nombre réel strictement positif.
On
s’intéresse maintenant à la fonction e représentant un signal de même
forme que celui de la partie A, mais dont la période, exprimée en
seconde, est 2t
et dont le graphe est représenté ci-après.
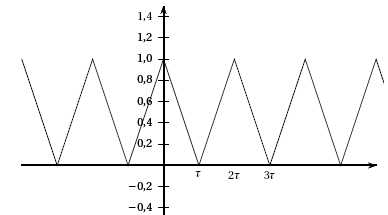
Ce signal est placé
en entrée
d’un filtre passe-bas (il s’agit d’un filtre de Butterworth d’ordre 6
et de fréquence de coupure 40 Hz). Le signal de sortie obtenu est
modélisé par une fonction h.
1.
On se place dans le cas où la fonction e est telle que t =
0,1.
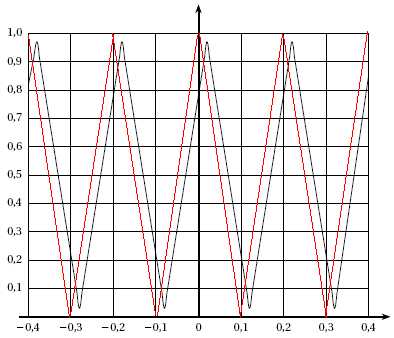
La
figure 1 du document réponse 1 donne une représentation graphique de la
fonction h sur l’intervalle [−0,4 ; 0,4], obtenue à l’aide
d’un
logiciel de simulation.
a. Déterminer
graphiquement la valeur maximale hmax de la
fonction h.
hmax = 0,97.
b.
Sur la figure 1 du document réponse 1, tracer la représentation
graphique de la fonction e.
c.
Le facteur de crête du signal h, exprimé en décibels, est défini par Fc
= 10 /ln10 ln(h2max /Ph).
On a obtenu à l’aide d’un logiciel de calcul numérique la valeur
approchée suivante de la puissance
moyenne par période Ph du signal h : Ph
= 0,33330.
En déduire une valeur approchée du facteur de crête Fc
.
Fc = 10
/ln10 ln(0,972 / 0,3333) =4,51.
|
|
|
|
2. On note G(w) le
gain, exprimé en décibels, du filtre passe-bas en fonction de la
pulsation w.
Le graphique ci-après donne une représentation graphique de la fonction
G pour les « petites » valeurs de la pulsation w.
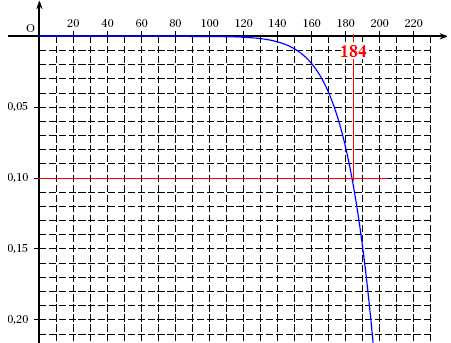
1. Déterminer
graphiquement l’intervalle des valeurs de w pour
lesquelles on a G(w)>=
-0,1 dB.
[0 ; 184 ].
On note w0
la solution de l’équation G(w)=
−0,1.
Déterminer, à 10−1 près, en précisant la
démarche suivie, une valeur approchée de w0.
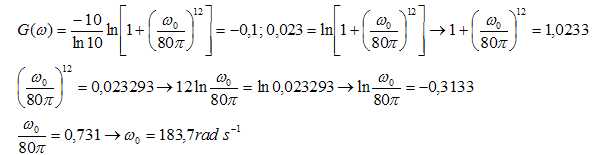
Exercice
2.
On note U la fonction échelon unité définie, sur l’ensemble des nombres
réels, par :
U(t) =0 si t <0 ; U(t) = 1 si t >=0.
Une
fonction définie sur l’ensemble des nombres réels est dite causale
lorsque cette fonction est nulle sur l’intervalle ]−oo; 0[.
On considère un système entée-sortie analogique du premier ordre dont
la fonction de transfert H est définie par :
H(p) =2/(1+0,5 p).
1. On
considère la fonction causale s dont la transformée de Laplace est :
S(p) =2 / [p(1+0,5p)].
La fonction s modélise la réponse du système analogique à l’échelon
unité U.
a. Vérifier que : S(p) =2 / p -2 /
(p+2).
S(p) =4 / [p(2+p)] =A / p + B /(p+2) = (p+2)A +Bp / [p(2+p)]
On identifie 2A=4 et 0 = A+B soit A = 2 et B = -2.
b. En déduire
s(t ) pour tout nombre réel t positif ou nul.
s(t) =2 U(t)-2e-2t U(t)= 2(1-e-2t).
c.
Compléter la ligne donnant les valeurs de s(t ) dans le tableau 2 du
document réponse 2 en donnant les valeurs approchées à 10−3 près.
| n | 0 | 10 | 20 | 30 | 40 | 50 | 100 | 150 | | y(n) | 0,039 |
| 1,119 | 1,410 |
| 1,735 |
|
| | t=0,02n | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | 2 | 3 | | s(t) | 0 | 0,659 | 1,101 | 1,398 | 1,596 | 1,729 | 1,963 | 1,995 |
2. On considère maintenant un système entrée-sortie numérique dont la fonction de transfert F est définie par
F(z)= H[100 (1-z-1) / (1+z-1)]
Ce système numérique permet d’approcher le système analogique.
L’entrée
et la sortie du système numérique sont modélisés, respectivement, par
deux suites causales x et y. Ces deux suites admettent des transformées
en Z notées, respectivement, X(z) et Y (z) telles que
Y (z)= F(z)X(z)
a. Montrer que F(z) = 2(1+z-1) / (51-49 z-1).
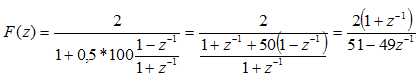
b. En déduire que 51Y (z)−49z−1Y (z)= 2X(z)+2z−1X(z).
Y(z)(51-49z-1)=2(1+z-1)X(z).
51Y (z)−49z−1Y (z)= 2X(z)+2z−1X(z).
c. En déduire que, pour tout nombre entier n supérieur ou égal à 0, on a :
y(n) =49 /51 y(n-1)+2 / 51 x(n) +2/51x(n-1).
51y(n) -49y(n-1) = 2x(n)+2x(n-1). Puis diviser par 51.
|
3. On suppose dans cette question que, pour tout nombre entier n, on a x(n) = d(n), où d est la suite impulsion unité définie par
(d(0) = 1 ; d(n) = 0 si n diffère de 0.
Grâce
à la formule obtenue dans la question 2c, compléter le tableau du
document réponse 2. On pourra utiliser des valeurs approchées à 10−3 près.
| n | -1 | 0 | 1 | 2 | 3 | | d(n) =x(n) | 0 | 1 | 0 | 0 | 0 | | y(n) | 0 | 0,0392 | 0,0769 | 0,0739 | 0,071 |
y(0) =49 / 51 y(-1) +2 / 51 x(0)+2 / 51 x(-1) =2 /51 =0,0392.
y(1) =49 / 51 y(0) +2 / 51 x(1)+2 / 51 x(0) =49 /51 *0,0392+2 /51 =0,0769.
y(2) =49 / 51 y(1) +2 / 51 x(2)+2 / 51 x(1) =49 /51 *0,0769 =0,0739.
y(3) =49 / 51 y(2) +2 / 51 x(3)+2 / 51 x(2) =49 /51 *0,0739 =0,0739.
4. Dans cette question, on suppose que, pour tout entier n, on a x(n) = e(n) où e est la suite échelon unité définie par
(e(n) = 0 si n < 0 ; e(n) = 1 si n >= 0
On admet que Y(z) =2z(z+1) / [(51z-49)(z-1)].
a. Vérifier que :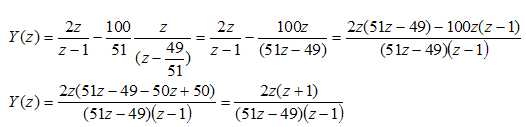
b. En déduire y(n) pour tout nombre entier naturel n.
y(n) = 2e(n) -100 / 51 (49 /51)n.
c. Compléter la ligne donnant les valeurs de y(n) dans le tableau du document réponse 2 avec des valeurs approchées à 10−3 près.
| n | 0 | 10 | 20 | 30 | 40 | 50 | 100 | 150 | | y(n) | 0,039 | 0,686 | 1,119 | 1,410 | 1,604 | 1,735 | 1,964 | 1,995 |
y(10) = 2*1 -100 /51 (49/51)10 =0,686.
y(40) = 2*1 -100 /51 (49/51)40 =1,604.
y(100) = 2*1 -100 /51 (49/51)100 =1,964.
y(150) = 2*1 -100 /51 (49/51)150 =1,995.
|
|