Lois normale,
binomiale, test d'hypothèse.
Bts 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
Partie 1 : Production de batteries
L’entreprise BatriPlus fabrique des batteries pour le téléphone Nova4
équipé du système d’exploitation OSNov7. Dans un souci de contrôle de
qualité de sa production, cette entreprise décide de procéder à un
contrôle de l’autonomie de ces batteries.
Le contrôle consiste à prélever une batterie au hasard dans la
production et, après l’avoir chargée et insérée dans un téléphone
Nova4, de procéder à un test d’autonomie.
Ce test est constitué d’une succession de visionnages vidéo, d’envois
de courriels, de conversations téléphoniques, . . . On détermine alors
l’autonomie en mesurant le temps écoulé entre le démarrage du test et
l’arrêt du téléphone par décharge de la batterie.
Une batterie est jugée conforme si l’autonomie est supérieure à 10,5
heures.
On modélise l’autonomie par une variable aléatoire X qui, à toute
batterie prélevée au hasard dans la production, associe son autonomie
en heures. On suppose que X suit la loi normale d’espérance m = 11,5 et
d’écart type s =
0,53.
Quelle est la probabilité qu’une batterie, prise au hasard dans la
production, soit jugée conforme ?
P(X >10,5) ; t = (m-10,5) / s
= (11,5-10,5) / 0,53 =1,88 7.
Les tables donnent P(1,887)
= 0,970.
La probabilité cherchée vaut : 0,97.
Partie 2 :
Commercialisation
La société PieceNov commercialise des lots de pièces détachées pour le
téléphone Nova4 auprès de revendeurs et de réparateurs. Elle
s’approvisionne pour 60%de ses batteries auprès de la société Batriplus
et pour le reste auprès de la société ElecBat.
On admet que 97%des batteries fabriquées par BatriPlus et 95%des
batteries fabriquées par ElecBat sont conformes.
1. On prélève une
batterie au hasard dans le stock pour la contrôler. On admet que toutes
les batteries ont la même probabilité d’être choisies.
Démontrer que la probabilité que la batterie soit non conforme est
0,038.
Batteries conformes : 0,60 *0,97 +0,40 *0,95 =0,962.
Probabilité pour qu'une batterie soit non conforme : 1-0,962 =0,038.
|
| .
. |
|
|
2. La société PièceNov commercialise
les batteries par lots de 60.
On choisit au hasard un lot de 60 batteries dans le stock. On admet que
le stock est suffisamment important pour que ce choix puisse être
assimilé à un tirage avec remise de 60 batteries.
On note Y la variable aléatoire qui, à chaque lot de batteries ainsi
prélevées, associe le nombre de batteries non conformes du lot.
a. Justifier que Y
suit une loi binomiale dont on donnera les paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 60. La
probabilité qu'une batterie soit non conforme est constante p = 0,038.
La probabilité qu'une batterie soit conforme est q = 0,962.
Y
suit la loi binomiale de paramètre n = 60 et p = 0,038.
b.
Calculer la probabilité qu’il y ait exactement 2 batteries non
conformes dans le lot.
p(Y=2)=C260 q58 p2 =60*59 / 2 *0,96258 *0,0382=0,270.
c.
Calculer la probabilité qu’il y ait plus de 4 batteries non conformes
dans le lot.
1-P(Y=0)-P(Y=1)-P(Y=2)-P(Y=3)-P(Y=5).
P(Y=0) = C060 q60 p0=0,96260 =0,0978.
p(Y=1)=C160 q59 p1 =60 *0,96259 *0,038=0,2319.
p(Y=3)=C360 q57 p3 =60*59*58 / 6 *0,96257 *0,0383=0,2064.
p(Y=4)=C460 q56 p4 =60*59*58*57 / 24 *0,96256 *0,0384=0,1162.
1-0,0978-0,2319-0,270-0,2064-0,1162
=0,0777~0,078.
d. Calculer E(Y ).
Que représente ce nombre dans le cadre d’un grand nombre de lots ?
E(Y) = np = 60*0,038 =2,28.
C'est le nombre moyen de batteries non conformes dans un lot de 60
batteries.
|
|
|
|
Partie 3.
Lors de la sortie du nouveau système d’exploitation OSNov8,
l’entreprise BatriPlus décide de contrôler l’autonomie des batteries
des téléphones Nov4 équipés du nouveau système. Le responsable de la
qualité désire alors savoir si l’utilisation de ce nouveau système
d’exploitation a réduit l’autonomie des batteries.
On construit un test d’hypothèse unilatéral pour savoir si, au seuil de
5%, on doit considérer que l’autonomie des batteries a diminué avec
l’utilisation du nouveau système d’exploitation.
Soit X la variable aléatoire qui, à chaque échantillon de 100 batteries
prélevées au hasard dans la production, associe son autonomie moyenne.
On admet que X suit une loi normale d’espérance m et d’écart type s = 0,053.
1. On choisit
l’hypothèse alternative H1 : «m < 11,5 ».
Donner l ’hypothèse nulle H0.
H0 : " m = 11,5".
2. Sous cette
hypothèse nulle, on obtient avec un tableur les résultats donnés
ci-dessous.
Déterminer une valeur approchée par défaut à 10−3 du réel a
tel que P (X >a) = 0,95.
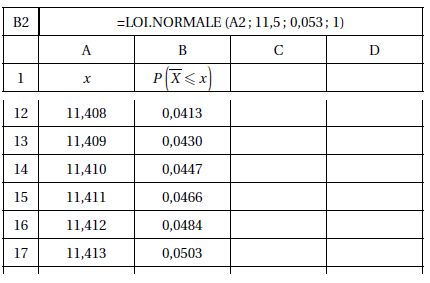
a =11,412.
3. Énoncer la règle
de décision du test.
Au seuil de 5% l'hypothèse H0 n'est pas vérifiée. Mais on ne
peut pas pour autant affirmer quelle a baissé.
On prélève dans le stock un échantillon de 100 batteries et on mesure
leur autonomie.
À l’issue des tests, l’autonomie moyenne des batteries de cet
échantillon est de 11,4 h.
4. Peut-on, au
seuil de 5%, considérer qu’avec l’utilisation du nouveau système
d’exploitation l’autonomie des batteries a baissé ?
Intervalle de confiance [ 11,4 -1,96 *0,053 /10 ; 11,4 +1,96 *0,053 / 10 ] soit
[11,3896 ; 11,410 ].
11,5 n'appartient à cet intervalle. Au risque de 5 %, on peut affirmer que l'autonomie a baissé.
5. Quelle aurait
été la conclusion si le test avait été réalisé au seuil de 1%?
2P(t)-1 =0,99 ; P(t) =1,99 / 2 = 0,995.
Les tables donnent t = 2,575.
Intervalle de
confiance [ 11,5 -2,575 / 10 *0,053 ; 11,5 +2,575 / 10 *0,053] soit [11,3863 ;
11,4136 ].
11,5 n'appartient à cet intervalle. Au risque de 5 %, on peut affirmer que l'autonomie a baissé.
|
|