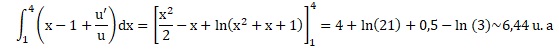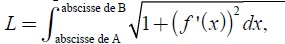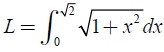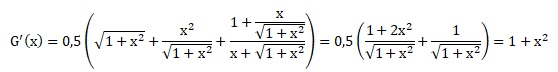Mathématiques,
Concours ingénieur territorial 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
1- Problème 1 (3,5 points )
Un
entrepreneur de travaux publics propose trois formules d'enrobé à chaud
à ses clients collectivités territoriales : l'enrobé de base (ERB),
l'enrobé bordé d'un trottoir (ERT) et la formule comprenant une piste
cyclable (ERC).
Pour chaque formule, le tableau ci-dessous indique le temps en heures
nécessaire à la pose de l'enrobé et les coûts brut et prix de vente
exprimés en 104 euros et ce pour 1 km.
|
ERT
|
ERC
|
ERB
|
coût brut
|
3
|
4
|
2
|
temps requis
|
8
|
10
|
6
|
prix de vente
|
12
|
16
|
10
|
Question 1 (2 points)
On considère la matrice M= et la matrice C.
1.a. Effectuer le produit matriciel MC.
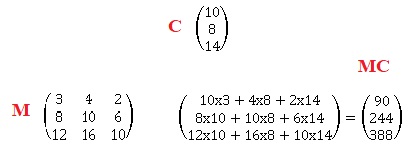
1.b.
Si pour la matrice C ,10 correspond à 10 Km d'ERT et 8 à 8 Km d'ERC et
enfin 14 à 14 Km d'ERB, donner la signification de chacun des
coefficients du produit matriciel MC. Vous exprimerez les sommes en
euros sans puissance de 10 et les temps en jours travaillés - sachant
qu'une journée travaillée dure 8 heures. (1,5 point).
90 : coût brut de 10 km d'ERT + coût brut de 8 km d'ERC +coût brut de 14 km d'ERB = 900 000 €.
244 : temps requis de 10 km d'ERT + temps requis de 8 km d'ERC +temps requis de 14 km d'ERB = 244 heures ou 30,5 jours.
388 : prix de vente de 10 km d'ERT + prix de vente de 8 km d'ERC +prix de vente de 14 km d'ERB = 3 880 000 €.
Question 2 (1,5 point)
On considère la matrice P et l'on admet que PM=I , I matrice unité.
Soit X et Y deux matrices à une colonne et trois lignes.
2.a. Démontrer que si MX = Y alors X = PY. (0,5 point)

2.b.
On sait que l'entreprise de TP a réalisé une recette de 4 300 000 € sur
un temps travaillé de 270 heures et avec un coût de un million d'euros.
Construire la matrice Y à partir de ces données, puis déterminer pour
chaque type d'enrobage le nombre de kilomètres réalisés. (1 point).
d=106 =100 104; e=270 ; f=4,3 106= 430 104.
3a +4b +2c = 100 (1) ; 8a+10b+6c = 270 (2) ; 12a +16b+10c = 430 (3)
4x(1) -(3) donne : 2c =30 ; c = 15 km.
3a +4b = 70 (1') ; 8a+10b = 180 (2') ;
2,5 x(1') -(2') donne : 7,5 a -8a =175-180 ; a = 10 km.
(1) donne : 4b = 100-30-30=40 ; b = 10 km.
|
| .
. |
...
|
|
Question 2 ( 3 points).
Une
salle philharmonique est vue de profil. La figure ABCD représente un
mur de cette salle dans un repère orthonormé d'unité un pour vingt cinq
mètres. On considère la courbe Ω d'équation y= f ( x) avec : f (
x)=x−1+(2x+1) / (x2+x+1) −ln ( x) et la courbe Φ d'équation y=ln ( x).
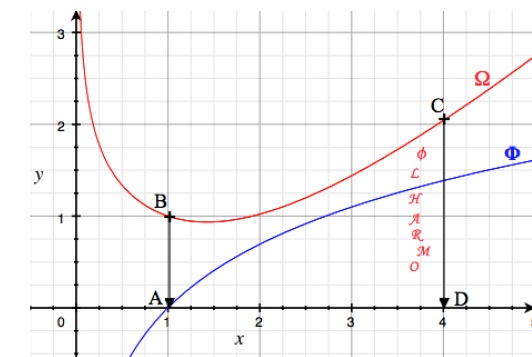
Question 1 (1 point)
On pose 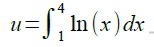 , donner une interprétation graphique de u et calculer ce réel u en
intégrant par parties. Donner le résultat en unités d'aire à 10−2 près par défaut.
, donner une interprétation graphique de u et calculer ce réel u en
intégrant par parties. Donner le résultat en unités d'aire à 10−2 près par défaut.
Aire comprise entre la courbe bleue F, l'axe des abscisses et les droites d'équation x=1 et x=4.
On pose u = ln(x) ; v' = dx ; u' = 1 /x ; v = x.
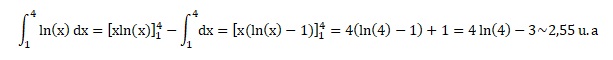
Question 2 (1 point)
2.a Calculer 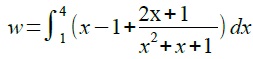 . Pour la suite on admettra que w=6,44 unités d'aire. . Pour la suite on admettra que w=6,44 unités d'aire.
On pose u = x2+x+1 ; u' = 2x+1.
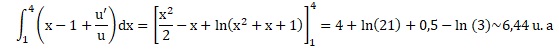
2.b Par linéarité de l'intégration on en déduit w-u, soit A1 l'aire concernant la portion de plan délimité par Ω , la courbe F et la bande 1⩽x⩽4.
On donnera une valeur approchée, en unités d'aire, à 10−2 près.
A1 = 6,44 -2,55=3,89 u.a.
Question 3 (1 point)
3.a Considérons l'aire A2 définie par A2=A1−u
Calculer A2 en unité d'aire puis donner le résultat en m2.
A2 = 3,89 -2,55 =1,34 u.a soit 1,34 x 252 =837,5 m2.
3.b Une peinture a un pouvoir couvrant de 1 litre pour 10 m2. 850 litres de peinture seront-ils suffisants pour recouvrir le mur délimité par l'aire A1 ? Justifier.
A1 correspond à 3,89 x252 ~2431 m2.
243 litres de peinture sont nécessaire pour couvrir l'aire A1.
|
....
|
Problème 3 . ( 3,5 points)
Deux routes se croisent perpendiculairement. Un chemin piétonnier mène d’une route à l’autre selon le schéma suivant :
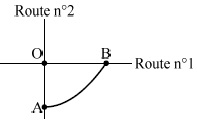
On choisit le repère d’origine O, le croisement des deux routes, d’axe
des abscisses la route n°1, d’axe des ordonnées la route n°2. L’unité
de longueur étant le kilomètre, le point A a pour coordonnées (0 ;-1)
et le point B a une abscisse positive et une ordonnée nulle.
Dans ce repère, le chemin piétonnier reliant A et B est un arc de la parabole P représentative de la fonction f (x) = 0,5x2 -1.
Partie A, longueur du chemin piétonnier (1,5 point).
On rappelle que la longueur L du chemin piétonnier est donnée, en unités de longueur, par l’intégrale :
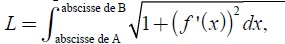
où f ' est la fonction dérivée de la fonction f.
1. Montrer que 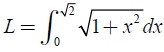
f '(x) =x ; 1+f '(x)2 = 1 +x2.
Montrer qu’une primitive, sur R, de la fonction g(x)= (1+ x2 )½ est :
G(x) = 0,5 [x(1+ x2 )½ +ln(x+(1+ x2 )½ )).
On dérive G(x) :
Dérivée de x(1+ x2 )½ : on pose u = x et v = (1+ x2 )½ ; u' = 1 ; v' = x(1+ x2 )-½ ;
u'v + v'u = (1+ x2 )½ +x2(1+ x2 )-½ ;
Dérivée de ln(x+(1+ x2 )½ ) : [1+x(1+ x2 )-½ ] / [x+(1+ x2 )½ ] ;
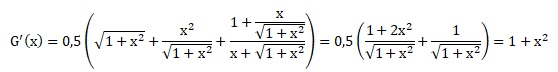
3. Calculer alors la longueur de ce chemin piétonnier ; la réponse finale sera arrondie au mètre près.
L =G(2½) - G(0) =0,5 [6½+ln(2½+3½)]-0,5[0+0] ~1,798 km.
Partie B, un cercle de courbure ou cercle osculateur (2 points)
On s’intéresse au cercle de courbure G de la parabole P au point C
d’abscisse 1 du chemin piétonnier, cercle de centre V représenté
ci-dessous :
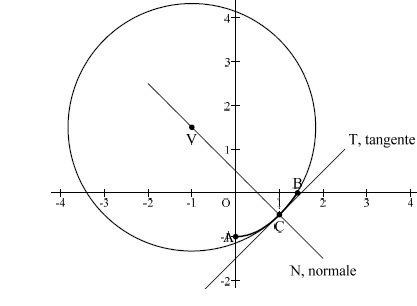
1. On rappelle que le rayon de courbure, rayon du cercle de courbure, de la parabole P en son point d’abscisse x est donné par :
R =(1+f '(x)2)1,5 / f ''(x).
où f " est la dérivée seconde de la fonction f.
Montrer que le rayon du cercle G est de 8½.
f '(x) =x ; f ''(x) = 1 ; R =(1+x2)1,5 avec x = 1 ; R = 21,5 =2 *2½ = 4½ *2½ = 8 ½.
2. Déterminer des équations de la tangente T et de la normale N à la parabole P au point C. (0,75 point)
Coefficient directeur de la tangente en C à la parabole : f '(1) = 1 ;
équation de T : y = x+b ; T passe au point C(1 ; f(1)) soit C(1 ; -0,5).
-0,5 = 1 +b ; b = -1,5 ; y = x-1,5.
Coefficient directeur de N : -1 ;
équation de N : y = -x+b ; N passe au point C(1 ;-0,5) ;
-0,5 = -1 +b ; b = 0,5. y = -x+0,5.
On rappelle que T et N se croisent perpendiculairement au point C.
3. Calculer les coordonnées du point V. (1 point)
VC2 = 8 ; (xC-xV)2 +(yC-yV)2 = 8 ; (1-xV)2 +(-0,5-yV)2 = 8 ;
De plus yV = -xV +0,5 ; (1-xV)2 +(1-xV)2 = 8 ; (1-xV)2 =4 ; 1-xV = 2 ; xV = -1 et yV =1,5.
|
|



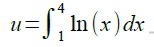 , donner une interprétation graphique de u et calculer ce réel u en
intégrant par parties. Donner le résultat en unités d'aire à 10−2 près par défaut.
, donner une interprétation graphique de u et calculer ce réel u en
intégrant par parties. Donner le résultat en unités d'aire à 10−2 près par défaut.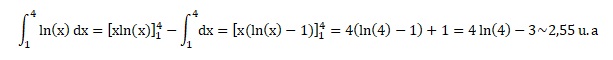
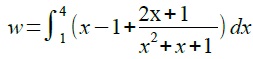 . Pour la suite on admettra que w=6,44 unités d'aire.
. Pour la suite on admettra que w=6,44 unités d'aire.