Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 27
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Soit g la fonction définie sur R par g(x))=e100x. Alors :
a) g est croissante sur R. vrai ; b) g est décroissante sur R ; c) g change de sens de variation sur R ;
d) aucune des propositions précédentes.
2. Soit f la fonction définie sur 𝐑 par f(x)=100x2+10x+1.
Dans le plan muni d’un repère orthogonal, la courbe représentative de
la fonction f est une parabole dont l’axe de symétrie a pour équation :
a) x = 10 ; b) x=10 ; c) x=0,05 ; d) x = -0,05 vrai.
x = -b / (2a) = -10 / 200 =-0,05.
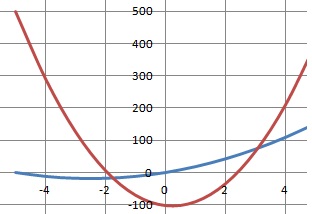
3. Soit a et b les fonctions définies sur 𝐑 par a(x)=3x2+15x+1 et b(x)=25x2+5x−100. Dans le plan muni d’un repère orthonormé les courbes représentatives des fonctions a et b ont :
a) aucun point d'intersection ; b) un point d'intersection ; c) 2 points d'intersection, vrai ; d) 4 points d'intersection.
3x2+15x+1 =25x2+5x−100 ; 22x2-10x−101=0 ; discriminant : (-10)2 -4*(-101)*22=8988.
Le discriminant est positif, donc 2 points d'intersection.
4. La somme 1+5+52+⋯+510 est égale à :
a) 2 441 406 ; b) 271 ; c) 555 ; d) 12 207 031. Vrai.
Somme des dix premiers termes d'une suite géométrique de raison 5 et de premier terme 1.
S = (1-511) /(1-5)=12 207 031.
5. Soit f la fonction définie sur 𝐑 dont la représentation graphique Cf est donnée ci-dessous. On sait de plus que la courbe Cf admet deux tangentes horizontales : une au point d’abscisse −1 et l’autre au point d’abscisse 3.
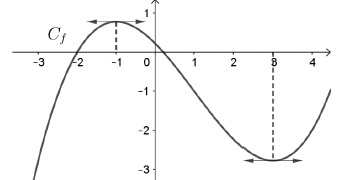
Alors le réel f ′(−1)xf ′(3) est :
a) strictement positif ; b) strictement négatif ; c) égal à 0 vrai ; d) égal à f ′(−3).
Si la tangente est horizontale, f '(-1) = f '(3) = 0.
Sujet 28.
1. La droite D de vecteur directeur de coordonnées (-3 ; 1) passant par A(−1 ; 2) a pour équation :
a) −3x+y−5=0 ; b) x+3y−5=0 ; c) x−3y−5=0; d) 3x+y+1=0.
Equation réduite y = -x / 3 +b.
La droite passe par A : 2 = 1 /3 +b ; b = 5 /3.
y = -x /3 +5 /3 soit 3y = -x+5 ; x+3y-5=0. Réponse b.
2. On considère la droite d d’équation 5x−8y+9=0. Alors :
a) A(6 ; 7) appartient à D. Faux. 5*6-8*7+9= -17 difère de zéro.
b) Le vecteur de coordonnées (5 ; 8) est un vecteur normal à D. Faux. ( il aurait fallu écrire ( 5 ; -8))
c) D coupe l’axe des ordonnées au point B(0;1). Faux.
y = 0 ; 5x+9=0 ; x = -9 / 5.
d) D est parallèle à la droite D′ d’équation 2,5x−4y+2=0.
Coordonnées d'un vecteur normal à D' ; ( 2,5 ; -4) ou (5 ; -8). Réponse d.
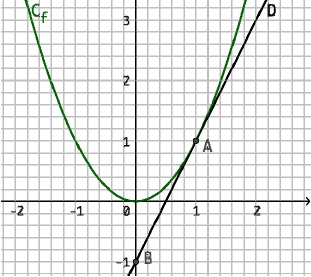
3. On considère la fonction f dont la représentation graphique Cf est donnée. La droite D est la tangente à Cf au point A(1;1). Le point B(0;−1) appartient à la droite D. Le nombre dérivé f ’(1) est égal à :
a) 1 : b)0,5 ; c) 2 ; d) -2.
(yB-yA) / (xB-xA) = -2 / (-1) = 2. Réponse c.
4. On considère une fonction f polynôme du second degré dont le tableau de signes est donné ci-après :

Une expression de f(x) peut être :
a) 2x2+5x−2 ; b) −x2+1 ; c) - x2+x+2 ; d) x2+x−2.
2*(-1)2 +5*(-1)-2 =-5 diffère de zéro ;
-22 +1 =-3 diffère de zéro.
-(-1)2+(-1)+2 =0 ; -22 +2+2=0. Réponse c.
5. On considère la fonction f définie sur R par f(x)=xex.
Alors la fonction dérivée de f, notée f ′ est définie sur R par :
a) f ′(𝑥)= ex ; b) f ′(𝑥)=(x+1)ex ; c) f ′(𝑥)=e ; d) f ′(x)= x2ex.
On pose u = x et v =ex; u' = 1 ; v' = ex.
u'v +v'u = ex+xex =(x+1)ex. Réponse b.
|
|
Exercice 2. ( 5
points) Sujet 27. Dans le plan muni d’un repère, on a tracé la courbe représentative Cf d’une fonction f définie et dérivable sur R. On note f ′ la dérivée de f. On sait que la courbe Cf admet exactement deux tangentes horizontales :
l’axe des abscisses comme tangente à la courbe Cf au point A(-1 ; 0) ;
la droite TB comme tangente à la courbe Cf au point B(1 / 3;−32 / 27).
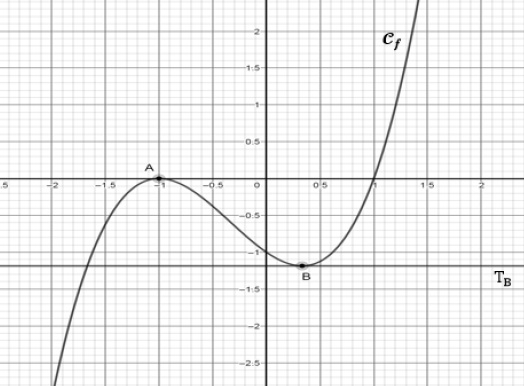
1. Par lecture graphique, donner les solutions de l’équation f(x)=0.
x = -1 et x = 1.
La fonction f est définie sur R par f(x)=x3+x2−x−1. On note f ′ la dérivée de f.
2. Déterminer f ′(x) pour tout réel x.
f '(x) =3x2+2x-1.
f '(x) s'annule pour x = 1 / 3 et x = -1.
f '(x) est négative sur ]-1 ; 1 /3[ ; f est décroissante.
f '(x) > 0 sur ]-oo ; -1[ union ]1 /3 ; +oo[ ; f(x) est croissante.
f '(-1) = f '(1/3) =0; f(x)présente deux extrémums.
3. En déduire le tableau de variations de f.
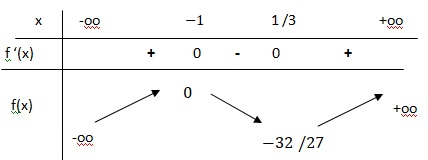
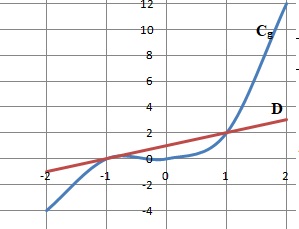
4. En utilisant ce qui précède, déterminer la position relative de la courbe Cg de la fonction g définie sur R par g(x)=x3+x2 et de la droite D d’équation y=x+1.
g(x) -y = x3+x2 -x-1= f(x).
f(x) > 0 si x > 1 : g(x) > y ; Cg est au dessus de la droite D.
f(x) < 0 si x < 1 : g(x) < y ; Cg est en dessous de la droite D.
Pour x = 1, la droite est tangente à Cg.
Sujet 28.
Dans
un aéroport, les portiques de sécurité servent à détecter les objets
métalliques que pourraient emporter certains voyageurs.
On choisit au hasard un voyageur franchissant un portique. On note :
S l’événement « le voyageur fait sonner le portique ».
M l’événement « le voyageur porte un objet métallique ».
On considère qu’un voyageur sur 500 porte sur lui un objet métallique.
On remarque que :
Lorsqu’un voyageur franchit le portique avec un objet métallique, la probabilité que le portique sonne est égale à 0,98.
Lorsqu’un voyageur franchit le portique sans objet métallique, la
probabilité que le portique ne sonne pas est aussi égale à 0,98.
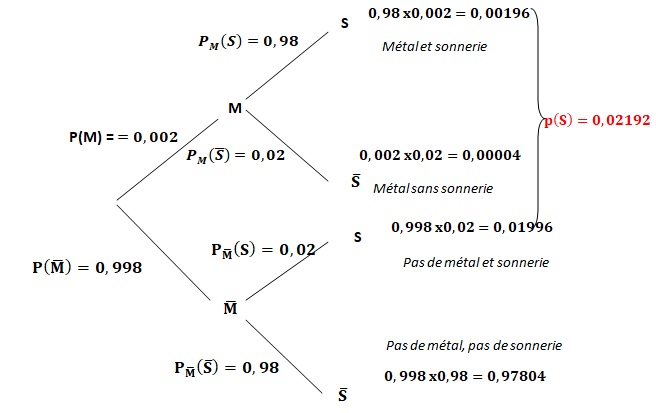
1. Recopier et compléter l’arbre de probabilités ci-dessous illustrant cette situation.
2. Montrer que : P(S)=0,021 92.
3. On suppose qu’à
chaque fois qu’un voyageur franchit le portique, la probabilité que ce
portique sonne est égale à 0,02192, et ce de façon indépendante des
éventuels déclenchements de sonnerie lors des passages des autres
voyageurs.
Deux personnes passent successivement le portique de sécurité. On note
X la variable aléatoire donnant le nombre de fois où le portique sonne.
a. Justifier qu’on peut modéliser la loi de X par une loi binomiale B(n, p) dont on précisera les paramètres n et p.
Les événements sont indépendants et conduisent à deux issues : sonnerie
avec une probabilité p = 0,02192 ou absence de sonnerie avec une
probabilité q = 1-p.
B(n, p) soit B(2, 0,02192).
b. Reprendre et compléter le tableau donnant la loi de X :
k
|
0
|
1
|
2
|
P(X=k)
|
00,95664
|
0,04288
|
0,00048
|
c Calculer et interpréter l’espérance de X dans le contexte de l’exercice.
E(X) =0,04288 +2 x 0,00048 =0,04384.
Ou encore E(X) = np = 2 x0,02192 =0,04384.
En moyenne, le portique sonne environ 44 fois lorsque 1000 personnes le franchissent.
|
|
Exercice 3. ( 5 points).
Sujet 27.
Dans cet exercice et si cela est nécessaire, les résultats seront arrondis à 0,1.
Le graphique ci-dessous illustre l’évolution du nombre (en milliers) de
voitures électriques immatriculées en France entre 2015 et 2018.
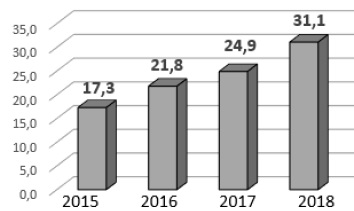
1. On
cherche à modéliser l’évolution du nombre (en milliers) de voitures
électriques immatriculées en France à compter de l’année 2015 à l’aide
d’une suite. On hésite entre deux modèles :
Premier modèle : on fait l’hypothèse que ce nombre augmente de 21 % par an. On définit alors une suite (un) où, selon ce modèle, un est le nombre (en milliers) de voitures électriques immatriculées en France l’année 2015+n avec n entier. Ainsi, on a u0=17,3.
Second modèle : on définit la suite (vn) par v0=17,3 et pour tout entier naturel n, vn+1=0,7vn+10. D’après ce modèle et pour tout entier naturel n, vn est le nombre (en milliers) de voitures électriques immatriculées en France l’année 2015+n.
a. Donner les valeurs des réels u1, u2, u3, v1, v2 et v3.
u1 =1,21 u0 =1,21 x17,3 =20,9 ; u2 =1,21 u1 =1,21 x20,3 =25,3 ; u3 =1,21 u2 =1,21 x25,3 =30,6 ;
v1 =0,7 v0 +10=22,1 ; v2 =0,7 v1 +10=25,5 ; v3 =0,7 v2 +10=27,8.
b.
Des deux modèles, lequel apparait le mieux adapté pour modéliser à
l’aide d’une suite l’évolution du nombre de voitures électriques
immatriculées en France à compter de l’année 2015 donnée dans le
graphique ? Argumenter.
Seul le premier modèle confirme les valeurs de l'histogramme.
2. Dans ce qui suit, on choisit de modéliser le nombre de voitures
immatriculées en France à compter de l’année 2015 à l’aide de la suite
(un) définie dans la question 1.
a. Donner la nature de la suite (un) et préciser sa raison.
C'est une suite géométrique de raison 1,21 et de premier terme u0=17,3.
b. Pour tout entier naturel n, exprimer un en fonction de n.
un = 17,3 x 1,21n.
c. On considère l’algorithme en langage Python ci-dessous.
u =17,3
n=0
while u < 50 :
u=1.21*u
n=n+1
Quelle est la valeur de la variable n à la fin de l’exécution de cet
algorithme ? Interpréter ce résultat dans le contexte de l’exercice.
un = 17,3 x 1,21n > 50.
u5 =44,87 ; u6=54,29.
A la fin de l'algorithme n = 6.
A partir de l'année 2015 +6 = 2021, le nombre de voitures électriques immatriculées dépassera 50 milliers en France.
Sujet 28.
En 2019, les déchets d'une entreprise sont évalués à 6 000 tonnes.
Cette entreprise s'engage à réduire ses déchets de 5 % chaque année.
1. Avec cette politique, quelle quantité de déchets peut envisager l'entreprise pour l'année 2020 ?
6000 x(1-5 /100)=6000 x0,95 =5700 t.
2. Pour tout entier naturel n, on note dn la quantité de déchets
produits en tonne par cette entreprise l'année 2019+n. Avec cette
notation, on a alors d0=6000.
a. Exprimer dn+1 en fonction de 𝑑𝑛 pour tout entier naturel n.
dn+1 = 0,95 dn.
b. Quelle est la nature de la suite (dn) ?
Suite géométrique de raison 0,95 et de premier terme d0 = 6000.
c.
Déterminer la quantité totale de déchets produits par l'entreprise
entre 2019 et 2023. On arrondira le résultat à la tonne près.
n = 4, somme des 4 premiers termes d'une suite géométrique :
S = 6000 (1-0,954) /(1-0,95) =22 959 t.
3. L'entreprise souhaite savoir au bout de combien d'années
d'application de cette politique de réduction des déchets la quantité
annuelle produite aura diminué de 40 % par rapport à la quantité
produite en 2019.
Recopier et compléter l'algorithme ci dessous sur la copie afin qu'il permette de répondre à la question posée :
6000-0,40 x 6000=6000 x0,6 =3600 t.
D=6000
N=0
Tant que D > 3600
D=0,95*D
N=N+1
Fin Tant que
|
|
Exercice 4. ( 5 points) Sujet 27 Un jeu est organisé à partir d’un sac contenant 6 jetons rouges et 4 jetons noirs. Les jetons sont indiscernables au toucher.
Un joueur prend deux jetons au hasard dans le sac selon le déroulé
suivant : le joueur prend un premier jeton au hasard dans le sac et
il met le jeton de côté ; le joueur prend un second jeton au hasard
dans le sac et il met le jeton de côté.
On note :
R1 l’événement « le premier jeton tiré est de couleur rouge » ;
R2 l’événement « le second jeton tiré est de couleur rouge ».
1. Recopier sur la copie et compléter l’arbre ci-dessous :
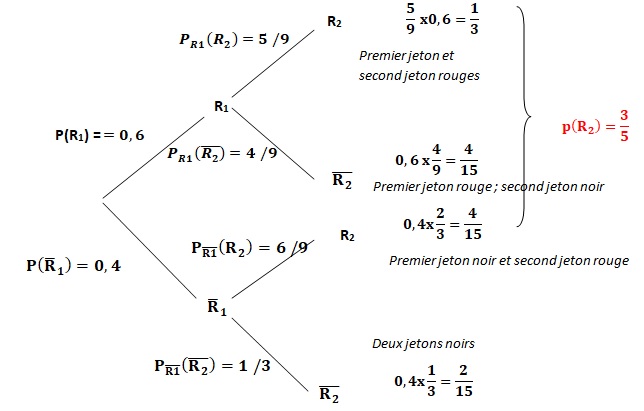
2. On considère l’événement A « le joueur obtient deux jetons de couleur rouge ».
a. Déterminer la probabilité p(A).
p(A) = 0,6 x5 / 9 = 1 / 3 ~0,33.
b. Décrire l’événement contraire de l’événement A par une phrase de la forme « le joueur obtient … » .
Le joueur n'obtient pas deux jetons de couleur rouge.
3. Montrer que la probabilité que le second jeton tiré soit de couleur rouge est égale à 0,6.
P(R )=0,6 x5 /9 +0,4 x6 / 9 =1 / 3 +8 /30 =18 /30 =6 /10 = 0,6.
4. Le second jeton
tiré est de couleur noire. Que peut-on alors penser de l’affirmation
suivante: « il y a plus de 50 % de chance que le premier jeton tiré ait
été de couleur rouge » ? Justifier la réponse.
Pnon R2( R1) = P(non R2 n R1) / P(non R2) =4 / 15 / (6 /15) =4 /6 = 2 /3. Affirmation vraie.
|
Sujet 28.
On
procède, chez un sportif, à l'injection intramusculaire d'un produit.
Celui ci se diffuse progressivement dans le sang. On admet que la
concentration de ce produit dans le sang (exprimée en mg/L =
milligramme par litre) peut être modélisée par la fonction f, définie
sur l'intervalle [0;10] par :
f(x)=6xe-x où x est le temps exprimé en heure.
Sa courbe représentative C est donnée ci dessous dans un repère orthonormé du plan.
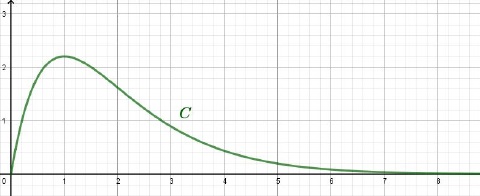
1. Montrer que pour tout x ∈[0;10], la fonction dérivée de f, notée f ', a pour expression : f '(x)=(6–6x) e-x.
On pose u = 6x et v = e-x ; u' = 6 ; v' = -e-x.
u'v+v'u = 6e-x-6x e-x.
2. Étudier le signe de f '′ sur [0;10] puis en déduire le tableau de variations de f sur [0;10].
e-x est toujours positif.
si x < 1 , f '(x) > 0 et f(x) est strictement croissante.
si x > 1 , f '(x) < 0 et f(x) est strictement décroissante.
Si x=1, f '(x) = 0 et f(x) présente un maximum.
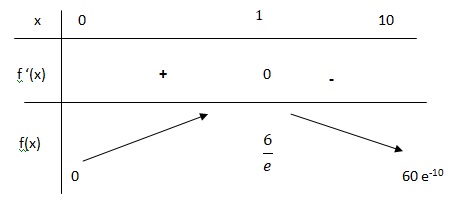
3. Quelle est la concentration maximale du médicament dans le sang ? (on donnera la valeur exacte et une valeur approchée à 10−1 près). Au bout de combien de temps est elle atteinte ?
Au bout d'une heure, la concentration maximale est égale à 6 / e ~2,2 mg / L.
4. Ce produit fait
l'objet d'une réglementation par la fédération sportive : un sportif
est en infraction si, au moment du contrôle, la concentration dans son
sang du produit est supérieure à 2 mg/L.
Le sportif peut il être contrôlé à tout moment après son injection ?
Expliquer votre raisonnement en vous basant sur l'étude de la fonction
et/ou une lecture graphique sur la courbe C.
Non car la concentration dépasse 2 mg / L entre environ 0,615 h( 37 min) et 1,52 h ( 91 min).
temps ( h)
|
0,615
|
0,8
|
1
|
1,2
|
1,4
|
1,52
|
concentration ( mg / L)
|
1,99
|
2,156
|
2,21
|
2,17
|
2,07
|
1,99
|
.
|
|