Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 33
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Dans un repère du plan, la droite (d) a pour équation : 2x – 3y + 1 = 0.
Un vecteur directeur de la droite (d) a pour coordonnés :
a) (2 ; −3) ; b) (3 ; 2) ; c) (−3 ; 1) ; d) (1; 1,5).
y = 2 / 3 x +1 /3 ; coefficient directeur de la droite : 2 /3 ; coordonnées du vecteur directeur : (1 ; 2 /3) ou (3 ; 2). Réponse b.
2. Dans un repère du plan, la droite (d) a pour équation : 2x – 3y + 1 = 0.
Un vecteur directeur de la droite (d) a pour coordonnés :
a) (2 ; −3) ; b) (3 ; 2) ; c) (−3 ; 1) ; d) (1; 1,5). Réponse a.
3. On donne trois points distincts : A, B et C.
Les points D et E sont tels que 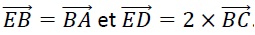 . On a : . On a :
a) A est le milieu de [EB] ; b) B est le milieu de [ED]
c) C est le milieu de [AD] ; d) D et le milieu de [AC]

4. Soit
x un nombre réel. Dans un repère orthonormé, les vecteurs de
coordonnées (−x + 4; 7) et (9; 2x − 5) sont orthogonaux lorsque x
est égal à :
a) 0,2 ; b) 10 ; c) -0,2 ; d) 6.
9(-x+4)+7(2x-5) = 0 ; -9x+36+14x-35=0 ; 5x+1=0 ; x = -1/5 = -0,2. Réponse c.
5. Dans
un repère orthonormé, on considère les points A(−1;−2), B(2;0), C(3;−1)
et D(−3;4). Alors le produit scalaire suivant est égal à :
a) −16 ; b) 11 ; c) 21 ; d) −24. Réponse a.
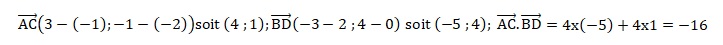 Sujet 34.
Sujet 34.
1. L'ensemble des solutions de l'inéquation −3x2+2x+1>0, où x est un nombre réel, est :
a) {−1/3 ; 1} ; B) ∅ ; c) ]−1/3 ; 1[ ; d) ]−∞;−1/3[∪]1;+∞[. Réponse c.
On cherche les solutions de : −3x2+2x+1 = 0 ; discriminant D = 22 -4*1*(-3)=16 = 42.
x1 = (-2 +4) / (-3*2) = -1/3 et x2 =(-2 -4) / (-3*2) =1.
a étant négatif, la parabole présente un maximum :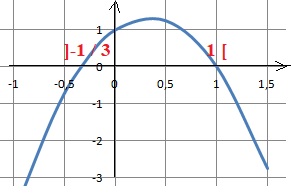
.
2. Le
plan est muni d'un repère. Une équation cartésienne de la droite (d)
passant par le point A de coordonnées (‒1 ; 5) et de vecteur directeur
de coordonnées (3 ; ‒2) est :
a) −2𝑥+3𝑦+13=0 ; b) −2𝑥−3𝑦−13=0 ; c) 2𝑥−3𝑦+13=0 ; d) −2𝑥−3𝑦+13=0
y = -2 / 3x +b.
A appartient à la droite ; yA = -2 / 3 xA +b ; 2 / 3 +b = 5 ; b = 5 -2 /3 = (15-2) / 3 = 13 /3.
y = -2 /3 x +13 / 3 soit : 3y +2x-13 =0 ou -3y -2x +13 = 0. Réponse d.
3. Soit f la fonction définie sur ]−∞;2[∪]2;+∞[ par f(x)=(2x+1) / (x−2).
La fonction dérivée de f ' est définie sur ]−∞;2[ ∪ ]2;+∞[ par :
a) f '(x) = 5 /(x-2)2 ; b) f '(x) = (3x-6) /(x-2)2 ; c) f '(x) = -3 /(x-2)2 ; d) f '(x) = -5 /(x-2)2 ;
On pose u = 2x+1 et v = x-2 ; u' = 2 ; v' = 1 ; (u'v-v'u) / v2 = (2(x-2)-(2x+1)) / (x-2)2 = -5 /(x-2)2 . Réponse d.
4. Pour tout nombre réel x, une expression simplifiée de (ex)2×e−𝑥+1 / e5𝑥 est :
a) e-4x+1 ; b) exp(x2-6x+1) ; c) exp(x2+4x+1) ; d) exp(-x3+x5-5x) . Réponse a.
ex×ex× e−𝑥+1 × e-5𝑥 =e-4x+1.
5. La fonction f est définie pour tout x réel par f (x)=ex(3ex−1).
La fonction dérivée de f est définie pour tout x réel par :
a) f ′(x)=ex(3ex) ; b) f ′(x)=6e2x−ex ; c ) f '(x) =3 e2x -ex ; d) f '(x)=3(ex)2-1.
On pose u = ex et v = 3ex-1 ; u' = ex ; v' =3ex ; u'v+v'u =ex(3ex-1)+3ex ex =ex (6ex -1)=6e2x-ex.
Réponse b.
|
|
Exercice 2. ( 5
points) Sujet 33. À partir d’un premier segment de 2 mm, on ajoute successivement un nouveau segment mesurant 150 % de la longueur du précédent.
Pour tout entier naturel n ≥1, on désigne par un la longueur, en mm, du n ième segment. Ainsi u1 = 2 et u2 = 3.
1. Déterminer u3 et u4.
u3 = 1,5 u2 =1,5 x3 =4,5 ; u4 = 1,5 u3 =1,5 x4,5 =6,75.
2. Pour tout entier naturel n supérieur à 1, exprimer un+1 en fonction de un.
En déduire la nature de la suite (un).
un+1 = 1,5 x un, suite géométrique de raison 1,5 et de premier terme 2.
3. Pour tout entier naturel n ≥1, exprimer un en fonction de n.
un = 2 x 1,5n-1.
4. On cherche à
déterminer à partir de combien de segments la longueur totale dépasse 1
mètre. On réalise pour cela un programme écrit en langage Python.
Recopier et compléter sur la copie ce programme pour qu’il affiche le
nombre attendu de segments.
i=1
u=2
longueur =2
while longueur < 1000 :
i = i+1
u = u*1,5
longueur =longueur +u
print (i)
5. Ce programme affiche 14. Déterminer, par le calcul, la longueur de
la spirale formée des 14 premiers segments. Arrondir le résultat au mm.
Somme des 14 premiers termes de la suite géométrique de raison 1,5 et de premier terme 2 :
S = 2 (1-1,514) /(1-1,5)~1164 mm.
Sujet 34.
Un
pépiniériste stocke un grand nombre d’arbustes de la famille des
viburnum en vue de les vendre. Ceux-ci sont de deux espèces différentes
: les viburnum tinus (nom commun : laurier
tin) et les viburnum opulus (nom commun : boule de neige). Il constate que :
- 80 % de ses arbustes sont des lauriers tins, les autres sont des boules de neige.
- Parmi les lauriers tins, 41 % mesurent 1m10 ou plus.
- Parmi les boules de neige, 32 % mesurent 1m10 ou plus.
1. Est-il vrai que moins de 15% des viburnum de ce pépiniériste sont des boules de neige de moins de 1m10 ?
0,20 x(1-0,32) =0,136, valeur inférieure à 0,15, l'affirmation est vraie.
On choisit au hasard un viburnum chez ce pépiniériste et on considère les événements suivants :
L : « le viburnum choisi est un laurier tin »
T : « le viburnum mesure plus de 1m10 ».
2. Décrire par une phrase la probabilité PL(non T). Décrire également par une phrase l’événement non L ∩ T.
PL(non T) : probabilité que le viburnum mesure moins de 1,10 m sachant que c'est un laurier tin.
non L ∩ T : le viburnum est un boule de neige et il mesure plus de 1,10 m.
3. Recopier et compléter sur la copie l’arbre de probabilité ci-dessous traduisant les données de l’énoncé.
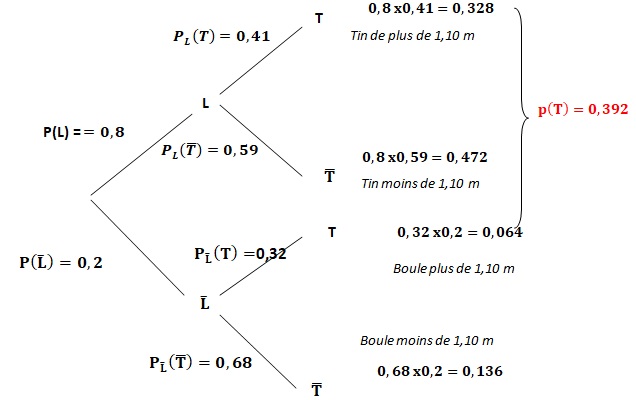
4. Montrer que la probabilité que le viburnum mesure 1m10 ou plus est égale à 0,392.
5. Le viburnum
choisi a une taille inférieure à 1m10. Quelle est la probabilité que ce
soit un boule de neige ? On arrondira le résultat à 10-3.
Pnon T (non L) = P(non T n non L) / P(non L) =0,136 /(0,136+0,472)=0,224.
|
|
Exercice 3. ( 5 points).
Sujet 33.
Un
libraire dispose d’un stock de magazines. On sait que 40 % des
magazines provient d’un fournisseur A et le reste d’un fournisseur B.
Il constate que 91 % des magazines reçus sont vendus dans la semaine.
Il constate également que 85 % des magazines provenant du fournisseur A sont vendus dans la semaine.
Le responsable des achats prend au hasard un magazine dans le stock. On considère les évènements suivants :
A : « le magazine provient du fournisseur A »
B : « le magazine provient du fournisseur B »
S : « le magazine est vendu dans la semaine »
1. Quelle est la probabilité que le magazine provienne du fournisseur B ?
P(B) = 0,6.
2. On note PB(S) =x, x ∈[0;1]. Recopier et compléter l’arbre pondéré ci dessous traduisant la situation :
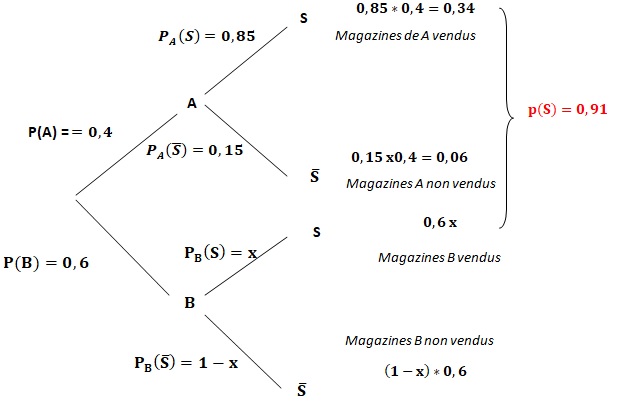
3. Calculer la probabilité que le magazine choisi au hasard provienne du fournisseur A et qu’il soit vendu dans la semaine.
P(A n S) =0,85 x0,4 = 0,34.
4. Démontrer que 0,34+0,6x=0,91. En déduire que P(B∩S)=0,57.
Formule des probabilités totales : P(S) = P(A n S) + P(B n S) = 0,34 +0,6x = 0,91 ;
P(B n S) =0,6x = 0,91-0,34 =0,57 soit x = 0,95.
5. Le magazine
choisi est vendu dans la semaine. Calculer la probabilité qu’il
provienne du fournisseur B. En donner sa valeur arrondie à 10−3.
PS(B) =P(B∩S) / P(S) = 0,57 / 0,91 =0,626.
Sujet 34.
Les deux parties suivantes sont indépendantes.
Partie A. On considère la suite (vn) définie par v0 = 1 et vn+1 =2 / 3 vn pour tout entier naturel n.
1. Quelle est la nature de la suite (vn ) ? En préciser les éléments caractéristiques.
Vn+1 / vn = 2 / 3 = constante. C'est une suite géométrique de raison 2 / 3 et de premier terme v0 =1.
2. Donner, pour tout entier naturel n, une expression de vn en fonction de n.
vn = v0 *(2 /3)n =(2 /3)n .
3. Calculer la somme S des dix premiers termes de la suite (vn).
S = v0(1-qn+1) / (1-q) =(1-(2 /3)10) / (1-2/3)~2,948.
Partie B. On modélise une suite (wn) à l’aide de la fonction suivante écrite en langage Python :
def terme (n) :
w=4
for i in range (n) ;
w = 2*w-3
return w
4. Que renvoie l’exécution de terme (5) ?
w1 = 4 ; w2 = 2 w1 -3 =8-3=5 ; w3 = 2 w2 -3 =10-3=7 ; w4 = 2 w3 -3 =14-3=11 ; w5 = 2 w4 -3 =22-3=19.
5.
En s’inspirant de la fonction terme(n), proposer une fonction
somme_termes(n), écrite en langage Python, qui renvoie la somme des n
premiers termes de la suite (wn).
def somme_termes (n) :
w=4
somme = w
for i in range (n) ;
w = 2*w-3
somme = somme +w
return w
|
|