Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 45
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Dans le plan muni d’un repère orthonormé, on considère les vecteurs decoordonnées respectives (−2,4) et (3,−6).
Le produit scalaire de ces deux vecteurs est égal à :
a. 18 ; b. −30 ; c. 0 ; d. 24 Réponse b.
-2x3+4x(-6) =-6-24 = -30.
2. On considère le triangle ABC tel que 𝐴𝐵=5, 𝐴𝐶=7 et l'angle BAC=60°.
Quelle est la longueur du côté BC ?
a. 𝐵𝐶=√109 ; b. 𝐵𝐶=√74 ; c. 𝐵𝐶=−35√3+74 ; d. 𝐵𝐶=√39. Réponse d.
BC2 = AB2+AC2-2*AB*AC*cos 60 =25+49-70 cos 60 = 74-35 =39.
3. Dans le plan muni d’un repère orthonormé, on considère le cercle C de centre 𝐴(2;3) et de rayon 𝑅=4.
Parmi les équations suivantes, laquelle est une équation du cercle C ?
a. 𝑥2+4𝑥+𝑦2+6𝑦+9=0
b. 𝑥2+4𝑥+𝑦2+6𝑦−3=0
c. 𝑥2−4𝑥+𝑦2−6𝑦−3=0
d. 𝑥2−4𝑥+𝑦2−6𝑦+9=0
Réponse c.
(x-2)2 +(y-3)2 = 42 ; x2-4x+4 +y2-6y+9 = 16 ; x2-4x +y2-6y-3 = 0.
4. Le réel −23π / 3 a le même point image sur le cercle trigonométrique que le réel :
a. −π / 3 ; b. π / 3 ; c. −2π / 3 ; d. 2π / 3.
Réponse b.
−23π / 3 = −24π / 3 +π / 3 = π / 3 -4*2π.
5. On considère l’algorithme suivant écrit en langage Python :
Liste(N):
U=1
L = [U]
for i in range (1 ; N):
U = 2*U+3
L.append(U)
return(L)
Que contient la variable L à la fin de l’exécution dans le cas où on choisit 𝑁 = 4 ?
a. [1, 5, 13, 29, 61] ; b. [1, 5, 13, 29] ; c. 61 ; d. 9. Réponse b.
Sujet 46.
1. On munit le plan du repère orthonormé.
On considère trois points du plan A, B et C tels que AB=2 ; AC =√3 et angle BAĈ=5𝜋 /6.
Alors le produit scalaire suivant est égal à :
a. 2√3 ; b. 3 ; c.− 2√3 ; d. – 3. Réponse d.
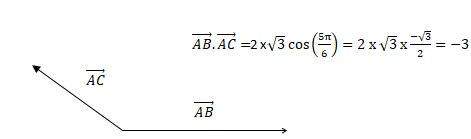
2. Soit a un nombre réel. On munit le plan du repère orthonormé.
On considère les vecteurs de coordonnées respectives (sin (𝑎) ; cos
(𝑎)) et (−cos (𝑎) ; sin (𝑎)). Alors le produit scalaire
de ces deux vecteurs est égal à :
a. sin2(𝑎)+ cos2(𝑎) ; b. 1 ; c. sin2(𝑎)− cos2(𝑎) ; d. 0. Réponse d.
sin(a) x(- cos(a)) +cos(a) x sin(a) = 0.
3. On munit le plan du repère orthonormé.
On considère les points A(2 ; 8), B(25 / 3 ; 0), C(7 ; −5) et D(3 ; 0).
Alors, les droites (AB) et (CD) sont :
a. parallèles ; b. perpendiculaires : c. sécantes ; d. confondues. Réponse c.
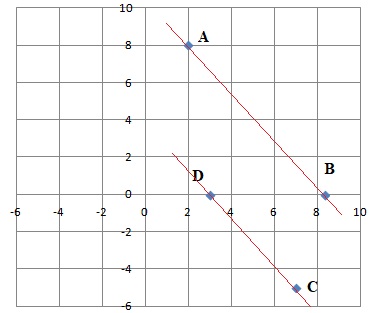
Coordonnées d'un vecteur directeur de la droite (AB): (0-8) / (25 / 3-2) = -24 /19 = -1,263.
Coordonnées
d'un vecteur directeur de la droite (CD): (0-(-5)) / ( 3-7) = -5 /4 =
-1,25, diffère de -1,263 ( droites non parallèles )
4. On munit le plan du repère orthonormé.
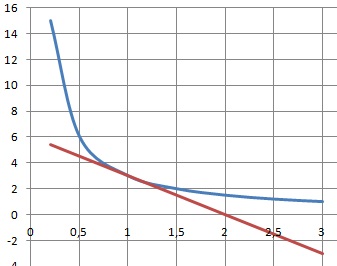
On considère la fonction 𝑓 définie pour tout réel 𝑥 non nul par
𝑓(𝑥)=3 / 𝑥. On note 𝒞 sa courbe représentative dans ce repère.
L’équation réduite de la tangente à 𝒞 au point d’abscisse 1 est :
a. 𝑦=−3𝑥+6 : b. 𝑦=−3𝑥 ; c. 𝑦=3𝑥 ; d. 𝑦=3𝑥+6. Réponse a.
f '(x) = -3 /x2 ; f '(1) = -3.
Equation réduite de la tangente : y = -3x+b.
Le point de coordonnées (1 ; f(1) =3) appartient à la tangente : 3 = -3+b ; b = 6.
5. L’ensemble des solutions dans R de l’équation 𝑥2=6𝑥−5 est :
a. 𝑆={1 ; 5} ; b. 𝑆={1} ; c. 𝑆=∅ ; d. 𝑆={−5 ; −1}.
x2-6x+5=0 ; discriminant D =(-6)2 -4*5=16 = 42 ;
x1 =(6-4) / 2 = 1 ; x2 =(6+4) / 2 = 5.
Réponse a.
|
|
Exercice 2. ( 5
points) Sujet 45. Une urne contient deux boules rouges et trois boules noires toutes indiscernables au toucher.
On tire au hasard une première boule en notant sa couleur puis on la remet dans l’urne.
On tire ensuite toujours au hasard une deuxième boule en notant sa couleur.
On note 𝑅 l’évènement « tirer une boule rouge » et 𝑁 l’évènement « tirer une boule noire ».
1. Recopier et compléter sur la copie l’arbre pondéré ci-dessous associé à cette expérience.
2. Quelle est la probabilité de tirer deux boules rouges ?
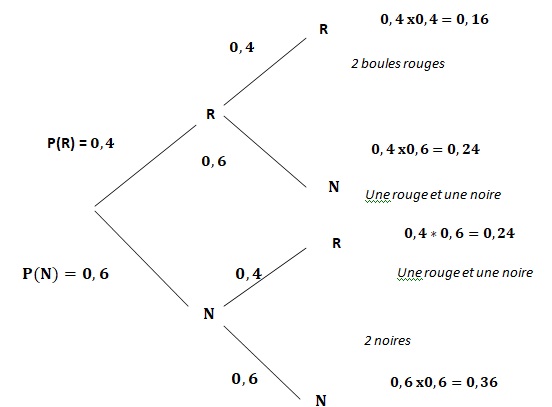
3. Si un joueur tire une boule rouge, il gagne 20 euros. S’il tire une boule noire, il perd 10 euros.
On note X la variable aléatoire égale au gain algébrique du joueur, en euros, à l’issue des deux tirages successifs.
Déterminer la loi de probabilité de la variable aléatoire X.
valeurs de X
|
40
|
10
|
-20
|
P(X) = a
|
0,16
|
0,48
|
0,36
|
4. Calculer la probabilité que le joueur gagne de l’argent.
1-036 = 0,64.
5. Calculer l’espérance de la variable aléatoire X et en donner une interprétation.
E =40*0,16 +10*0,48-20*0,36=6,4+4,8-7,2=4.
En moyenne, on gagne 4 €.
Sujet 46.
Maxime participe à un jeu qui se déroule en deux parties :
- La probabilité qu’il gagne la première partie est de 0,2.
- S’il gagne la première partie, il gagne la deuxième avec une probabilité de 0,9.
- S’il perd la première partie, il perd la suivante avec une probabilité de 0,6.
On note :
𝐺1 l’événement « Maxime gagne la première partie »
𝐺2 l’événement « Maxime gagne la seconde partie »
Partie A.
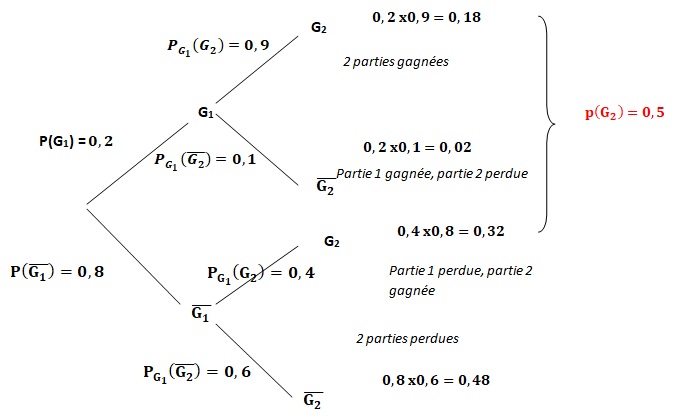
1. Construire un arbre pondéré illustrant la situation.
2. Calculer la probabilité que Maxime gagne les deux parties du jeu.
3. Montrer que la probabilité que Maxime gagne la deuxième partie du jeu est 0,5.
Partie B.
On sait de plus que :
- à chaque partie gagnée, le joueur gagne 1,5 €.
- à chaque partie perdue, il perd 1 €.
On note 𝑋 la variable aléatoire qui correspond au gain algébrique en euros de Maxime à l’issue des deux parties.
1. Compléter le tableau ci-dessous donnant la loi de probabilité de la variable aléatoire 𝑋.
valeurs de X
|
-2
|
0,5
|
3
|
probabilité
|
0,48
|
0,34
|
0,18
|
2. Déterminer si ce jeu est équitable. Justifier.
Espérance de X : -2 x0,48 +0,5 x0,34 +3 x0,18 = -0,96 +0,17 +0,54 = -0,25.
Le jeu n'est pas équitable, on perd plus souvant de l'argent que l'on gagne de l'argent.
|
|
Exercice 3. ( 5 points).
Sujet 45.
On considère les suites (𝑢𝑛)𝑛≥0 et (𝑣𝑛)𝑛≥0 définies par 𝑢0=7 et, pour tout entier naturel 𝑛, 𝑢𝑛+1=0,5𝑢𝑛+3 et 𝑣𝑛=𝑢𝑛−6.
1. Montrer que la suite (𝑣𝑛)𝑛≥0 est une suite géométrique de raison 0,5 et de premier terme 1.
vn+1 =un+1-6 =0,5un+3-6=0,5 un-3 =0,5(un-6) =0,5 vn.
v1 = u1-6=0,5 u0+3-6 =0,5u0-3=0,5* 7-3 = 0,5.
v1 = 0,5 v0 ; v0 =2 v1=2*0,5 = 1.
2. Pour tout entier naturel 𝑛, exprimer 𝑣𝑛 en fonction de 𝑛.
vn = v0 x0,5n =0,5n .
3. En déduire, pour tout entier naturel 𝑛, une expression de 𝑢𝑛 en fonction de 𝑛.
un = vn+6 =0,5n+6.
4. On note 𝑆=𝑣0+𝑣1+⋯+𝑣100 la somme des 101 premiers termes de la suite (𝑣𝑛)𝑛≥0.
a. Déterminer la valeur de S.
S = (1-0,5101) /(1-0,5)=1,9999.
b. En déduire la valeur de la somme des 101 premiers termes de la suite (𝑢𝑛)𝑛≥0.
S+101*6=607,999999.
Sujet 46.
Une personne souhaite louer une maison à partir du 1er janvier 2020 et a le choix entre deux formules de contrat :
Contrat n°1 : le loyer augmente chaque année de 200 €.
Contrat n°2 : le loyer augmente chaque année de 5 %.
Pour tout entier naturel 𝑛, on note :
𝑢𝑛 le loyer annuel de l’année 2020 + 𝑛 pour le contrat n°1.
𝑣𝑛 le loyer annuel de l’année 2020 + 𝑛 pour le contrat n°2.
Dans les deux cas, le loyer annuel initial est de 3600 €. On a donc 𝑢0=𝑣0= 3600.
1. Étude de la suite (𝑢𝑛)
a) Déterminer le loyer annuel de l’année 2021 pour le contrat n°1.
3600 +200 = 3800 €.
b) Déterminer l’expression de 𝑢𝑛 en fonction de 𝑛 puis en déduire le loyer annuel de l’année 2030.
un = u0 +200 n = 3600 +200 n
u10 =3600 +2000 = 5600 €.
2. Étude de la suite (𝑣𝑛)
a) Déterminer le loyer annuel de l’année 2021 pour le contrat n°2.
v1 =3600 x1,05 =3780 €.
b) Déterminer l’expression de 𝑣𝑛 en fonction de 𝑛 puis en déduire le loyer annuel de l’année 2030.
vn = 3600 x1,05n.
v10 = 3600 x1,0510 =5864,02 €.
3. On considère le script suivant, écrit en langage Python :
u =3600
v=3600
n=0
while u >=v :
u = u+200
v =1,05*v
n=n+1
Après exécution, la variable 𝑛 contient la valeur 6. Donner une interprétation de ce résultat dans le contexte de l’exercice.
A partir de 2026, le loyer du contrat n°1 est inférieur au loyer du contrat n°2.
|
|
Exercice 4. ( 5 points) Sujet 45 Soit 𝑓 la fonction définie sur l’ensemble R des nombre réels par 𝑓(𝑥)=3𝑥3−5𝑥2+2.
On note 𝐶𝑓 sa courbe représentative dans un repère du plan.
1. On admet que 𝑓est dérivable sur R et on note 𝑓 ′ sa fonction dérivée.
Donner l’expression de 𝑓 ′(𝑥), pour tout nombre réel 𝑥.
f '(x) =9x2-10x.
2. On note 𝑇 la tangente à 𝐶𝑓 au point d’abscisse −1. Donner l’équation réduite de la tangente 𝑇.
Equation réduite : y = a x+b avec a = f '(-1) = 19.
Le point de coordonnées (-1 ; f(-1) = -6 ) appartient à T : -6 = -19 +b ; b = 13.
y = 19x+13.
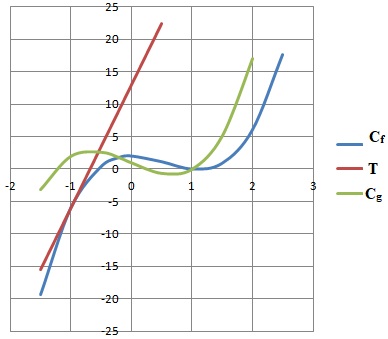
3. Soit 𝑔 la fonction définie sur R par 𝑔(𝑥)=3𝑥3−4𝑥+1.
On note 𝐶𝑔 sa courbe représentative dans le même repère que la courbe 𝐶𝑓.
a. Montrer que pour tout nombre réel 𝑥, 𝑓(𝑥)−𝑔(𝑥)=−5𝑥2+4𝑥+1.
f(x)-g(x)=3𝑥3−5𝑥2+2-3𝑥3+4𝑥-1 =−5𝑥2+4𝑥+1.
b. Étudier sur R le signe de 𝑓(𝑥)−𝑔(𝑥).
Racines de −5𝑥2+4𝑥+1 = 0 ; discriminant D = 42-4*1*(-5) =36 = 62.
x1 =(-4-6) / (-10)= 1 ; x2 =(-4+6) /(-10) = -0,2.
c. En déduire pour quelles valeurs de 𝑥 la courbe 𝐶𝑓 est au-dessus de la courbe 𝐶𝑔.
𝑓(𝑥)−𝑔(𝑥) > 0 pour x appartenant à ]-0,2 ; 1[.
|
Sujet 46.
Des pucerons envahissent une roseraie.
On introduit alors des coccinelles, prédatrices des pucerons, à
l’instant 𝑡=0, et on s’intéresse à l’évolution du nombre de pucerons à
partir de cet instant et sur une période de 20 jours.
Partie A :
Dans le repère ci-dessous, on a tracé :
La courbe 𝒞 représentant le nombre de milliers de pucerons en
fonction du nombre de jours écoulés depuis l’introduction des
coccinelles.
La tangente 𝑇 à la courbe 𝒞 au point d’abscisse 0 passe par les points 𝐴(0 ; 2,1) et 𝐵(2 ; 4,3).
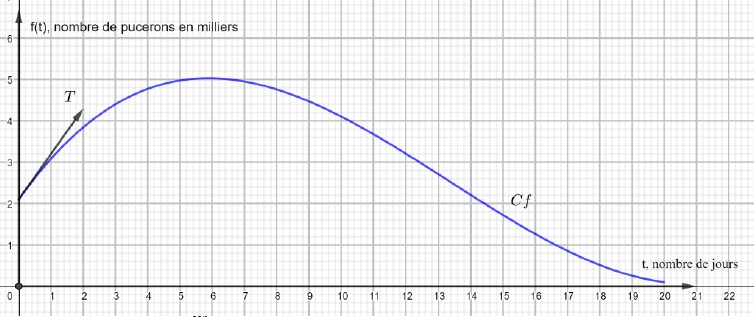
1. Déterminer par
lecture graphique le nombre de pucerons à l’instant où l’on introduit
les coccinelles puis le nombre maximal de pucerons sur la période de 20
jours.
2 100 pucerons à t = 0 et 5000 pucerons à t = 6 jours.
2. On assimile la vitesse de prolifération des pucerons à l’instant 𝑡 au nombre dérivé 𝑓′(𝑡).
Déterminer graphiquement la vitesse de prolifération des pucerons à l’instant 𝑡=0.
(4300 -2100) / 2 = 2 200 pucerons / jours.
Partie B :
On modélise l’évolution du nombre de pucerons par la fonction 𝑓 définie, pour tout 𝑡 appartenant à l’intervalle [0 ;20], par :
𝑓(𝑡)=0,003𝑡3−0,12𝑡2+1,1𝑡+2,1
où 𝑡 représente le nombre de jours écoulés depuis l’introduction des coccinelles et 𝑓(𝑡) le nombre de pucerons en milliers.
1. Déterminer 𝑓′(𝑡) pour tout 𝑡 appartenant à l’intervalle [0 ; 20] où 𝑓’ désigne la dérivée de la fonction 𝑓.
f '(t) = 0,009t2 -0,24t+1,1.
2. Dresser le tableau de signes de 𝑓′(𝑡) sur l’intervalle [0 ; 20].
Racines de 0,009t2 -0,24t+1,1 = 0 : discriminant D =(-0,24)2 -4*1,1*0,009 =0,0576-0,0396=0,018~0,1342.
Solution positive retenue : (0,24 -0,134) / 0,018 ~5,9 jours.
f '(t) > 0 si t appartient à [0 ; 5,9] et f '(t) < 0 si t appartient à [5,9 ; 20 ].
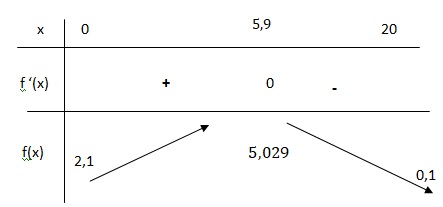
3.
En déduire le tableau des variations de la fonction 𝑓 sur l’intervalle
[0 ; 20]. Préciser les images des valeurs de 𝑡 apparaissant dans le
tableau.
|
|