Mathématiques,
(exercices 9 à 16 ), concours Puissance alpha 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Exercice 9 : petite étude de suite.
Pour tout entier naturel n, on pose :
- (un ) la suite de terme général un+1 = e un½ et de 1er terme u0 = 1.
- (vn ) la suite de terme général vn = ln(un )−2.
- (Sn ) la suite de terme général Sn = v0 + v1 +···+ vn
a) La suite (vn ) est une suite géométrique de raison q = 0,5. Vrai.
ln(un+1 )=ln(e un½ )=ln(e) + 0,5 ln(un)= 1+0,5 ln(un).
vn+1 =1+0,5 ln(un) -2 = -1 +0,5 ln(un) =0,5 ( ln(un) -2) = 0,5 vn.
b) Pour tout entier naturel n, vn =
1
/ 2n
. Faux.
v0 =ln(u0)-2=ln(1)-2= -2.
vn = v0 x 0,5n = -2 x 0,5n= -2 / 2n = -1 / 2n-1.
c) Pour tout entier naturel n, un =
e
2
/ e
1/
(2n−1)
. Vrai.
vn +2= -1 / 2n-1+2 = ln(un).
un = exp [-1 / 2n-1+2]= e2 / exp (1 / 2n-1).
d) La suite (Sn ) converge vers 2 . Faux.
Sn =v0 x(1-qn+1) / (1-q) = -2 ( 1-0,5n+1) / 0,5 = -4( 1-0,5n+1).
-1 < 0,5 < 1, donc 0,5n+1tend vers 0 si n tend vers plus l'infini.
La suite (Sn ) converge vers -4
Exercice 10 : Un peu de logiqur avec les suites.
(un) est une suite géométrique de terme général un et de raison q un nombre réel.
a) La suite (un ) est strictement croissante si et seulement si q > 1. Faux.
un = u0 qn ; un+1 = u0 qn+1 ; un+1-un = u0 qn (q-1).
u0 qn (q-1).>0 si : u0 >0 et q >1.
b) Si la suite (un ) est croissante alors un tend vers plus l'infini si n tend vers plus l'infini. Faux.
Si q = 0,5 et u0 = -1 : un+1-un = u0 qn (q-1) >0 et la suite est croissante.
Par contre un = - 0,5n tend vers zéro si n tend vers plus l'infini.
c) La réciproque du b) est fausse. Faux.
Réciproque de b. " Si n tend vers plus l'infini, un tend vers plus l"infini, alors la suite est croissante ".
un+1-un = u0 qn (q-1).
u0 qn (q-1).>0 si : si u0 >0 et q >1 , alors la suite est croissante .
d) La contraposée du b) est vraie. Faux.
Contraposée de b. " Si n tend vers plus l'infini, un tend vers plus l"infini, alors la suite est croissante ".
Excecice 11 : calculs de limites.
a. Pour n > 1, la suite de terme général un = (2n+1) / (1-2n) diverge. Faux.
un = 2n(1+1 / 2n) / [2n(1 / 2n-1)]=(1+1 / 2n) / (1 / 2n-1).
En plus l'infini, 1 / 2n tend vers zéro et un tend vers -1.
b) Pour n > 2, la suite de terme général vn = (n - 2 sin(n) / (1-n2) diverge. Faux.
vn =n2 (1 / n - 2 sin(n) / n2) / [n2(1/n2-1)] =(1 / n - 2 sin(n) / n2) / (1/n2-1)
En plus l'infini : 1 / n2 tend vers zéro et un tend vers 0.
c) La limite en plus l'infini de x / e2x+1 est égale à zéro. Faux.
x / e2x+1 =0,5 (2x / e2x)+1.
Par croissance comparée, en plus l'infini 2x / e2x tend vers zéro et x / e2x+1 tend vers 1.
d) La limite quand x tend vers e de (ln(x)-1) / (x-e) = 1 / e. Vrai.
La fonction f(x) = ln(x) est définie sur ]0 ; +oo[.
Pour tout a >0, quand x tend vers a, la limite de (f(x) - f(a)) / (x-a) = f '(a).
f '(x) = 1 /x tend vers 1/ e si a = e.
Exercice 12. Calculs d'intégrales.

|
....
|
Exercice 13. Distance d'un point à un plan.
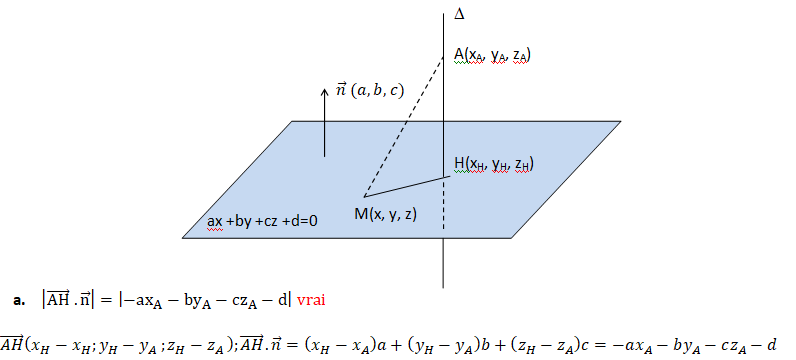
b. La distance du point A au plan est égale à AH = |axA+byA+czA+d| / (a2 +b2 +c2)½. Vrai.
b. AH x n = |axA+byA+czA+d| ; n = (a2 +b2 +c2)½.
ABCDEFGH est un cube tel que AB = 1.
I est le centre du carré EFGH.
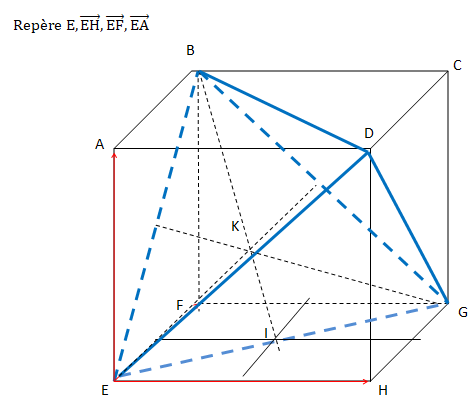
c) 0,5x-0,5y+0,5z =0 est une équation cartésienne du plan (BEG). Vrai.
E(0 ; 0 ; 0) appartient à ce plan : axE+byE+czE+d= 0 conduit à d = 0.
B(0 ; 1 ; 1) appartient à ce plan : axB+byB+czB= 0 conduit à b = -c.
G(1 ; 1 ; 0) appartient à ce plan : axG+byG+czG= 0 conduit à a = -b=c.
Equation de ce plan : x-y+z=0 ou 0,5x-0,5y+0,5z =0.
d) Le volume V du tétraèdre DBGE est égale à V = 1 /3.
Aire su triangle BEG : EG x BI / 2. = EI x BI.
EI = 2½ / 2 ; B(0 ; 1 , 1) ; I(0,5 ; 0,2) ; BI = (0,52 +0,52+12)½ =1,5½.
Aire su triangle BEG =3½/ 2.
Hauteur DK du tétraèdre issue de D :
K appartient au plan BEG : xK-yK+zK =0.
DK= |xD-yD+zD | / (12 +12 +12)½ = 2 / 3½.
V = 1 / 3 aire de base fois hauteur = 1 / 3 x3½ / 2 x2 /3½ =1 /3.
Exercice 14. Etude d'une
fonction logarithme.
f(x) = (1 +ln(x)) / (x-1)2 ; g(x) = -x-1-2x ln(x).
. a) Le domaine de définition de f est ]0 ; +oo[ ; le domaine de définition de g est ]0 ; +oo[. Faux.
Le domaine de définition de f est ]0 ; 1 [ union ]1 ; +oo[.
Le domaine de définition de g est ]0 ; +oo[.
b) g'(x) = - 2 ln(x) -3 et g admet e-1,5 comme maximum. Faux.
Dérivée de x ln(x) : on pose u =x et v = ln(x) ; u' = 1 ; v' = 1 /x.
u'v+v'u = ln(x) +1.
g'(x) = -1-2ln(x) -2 = -3 -2 ln(x).
g'(x) = 0 : -3 -2 ln(x). =0 ; ln(x) = -1,5 ; x = e-1,5.
g'(x) >0 si -3 -2 ln(x) >0 ; ln(x) > -1,5 et x > e-1,5 ; g(x) est strictement croissante sur ]0 ; e-1,5 ].
g(x) est strictement décroissante sur [ e-1,5 ; +oo[.
g admet un maximum en x = e-1,5 ; ce maximum vaut -e-1,5-1-2e-1,5 ln(e-1,5).
c) La courbe représentative de f admet une asymptote horizontale et deux asymptotes verticales. Vrai.
La droite d'équation x = 1 est asymptote verticale.
La droite d'équation x = 0 est asymptote verticale.
Quand x tend vers plus l'infini, f(x) tend vers 0 : l'axe des abscisses est asymptote horizontale.
d. f '(x) = g(x) / (x(x-1)3]. Vrai.
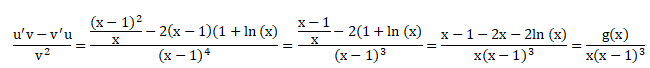
Exercice 15 : notions de base sur les complexes.
a. (3½+i)2 = 2+2 *3½ i. Vrai.
3+i2+2 *3½i =3 -1+2 *3½i =2+2 *3½ i.
z1 = 1+i *3½ ; z2 = 1-i ; Z = z25 / (conjugué de z1)4.
b. z1 / z2 = 2½ exp(7 i p /12). Vrai.
|z1| =(1+3)½ = 2 ; z1 / |z1| =0,5 + i *3½ / 2 = cos(p/3) +i sin (p/3) , z1 = 2 exp(i p /3).
|z2| =(1+1)½ = 2½ ; z2 / |z2| =1 / 2½ - i / 2½ = cos(-p/4) +i sin (-p/4) , z2 = 2½ exp( -i p /4).
z1 / z2 = 2½ exp( i (p /3 + p /4)) = 2½ exp(7 i p /12).
c) cos(7 p /12)= (2½-6½) / 4 et sin(7 p /12)= (2½+6½) / 4. Vrai.
z1 / z2 = (1+i *3½) / (1-i) = (1+i *3½)(1+i) / (1-i2)=[1 +i2*3½ +i(1+3½] / 2 =[1 -3½ +i(1+3½] / 2.
z1 / z2 =2½ exp(7 i p /12)= 2½ [cos(7 i p /12)+i sin(7 i p /12)].
On identifie : cos(7 i p /12) =(1 -3½) / (2*2½ )= (2½-6½) / 4.
sin(7 p /12)=(1+3½] / (2*2½ )= (2½+6½) / 4.
d) Z = 2½ / 4 exp(i p /12). Vrai.
(conjugué de z1)4 = 24exp( -i 4p / 3).
z25 =22,5 exp( -i 5p / 4)).
Z =22,5 exp( -i 5p /4+i 4p / 3) / 24 =2-1,5exp( i p /12)=2½ / 4 exp( i p /12).
Exercice 16 : géométrie et nombres complexes.
A, B, C et M sont les points d'affixes respectives zA = -1+i, zB =0,5 i, zC = -0,25 +1,25 i et z=x+iy avec x et y deux réels.
Soit f définie pour tout nombre complexe différent de zA par f(z) = (2z-i) / (z+1-i).
a) La partie réelle de f(z) est Re(f(z)) = (2x2+2x+2y2-3y+1) / [(x+1)2 +(y-1)2]
et la partie imaginaire de f(z) est égale à im(f(z)) = (x+2y-1) / [(x+1)2 +(y-1)2]. Vrai.
f(z) = (2x+i(2y-1)i) / (x+1+i(y-1)).
f(z) = (2x+i(2y-1) ) (x+1-i(y-1)) / [(x+1+i(y-1)) (x+1-i(y-1)].
(2x+i(2y-1)) (x+1-i(y-1)) =2x(x+1) -i2(2y-1)(y-1) +i[(x+1)(2y-1)-2x(y-1)] =2x2+2x+2y2-3y+1 +i(2xy-x+2y-1-2xy+2x).
(x+1+i(y-1)) (x+1-i(y-1) = (x+1)2 -i2(y-1)2 =(x+1)2 +(y-1)2.
.
b) L'ensemble des points M tel que f(z) soit un nombre réel est un cercle privé d'un point. Faux.
im(f(z)) doit être nulle soit x+2y-1 =0.avec x différent de -1 et y différent de 1.
Doite d'équation x+2y-1 =0 privée du point A.
c) L'ensemble des points M tel que f(z) soit un imaginaire pur est une droite privée d'un point. Faux.
Re(f(z)) doit être nulle soit . (2x2+2x+2y2-3y+1) avec x différent de -1 et y différent de 1 ( point A exclu)..
x2+x+y2-1,5y+0,5=0.
(x+0,5)2 -0,25 +(y-0,75)2 -0,752+0,5 = 0.
(x+0,5)2 +(y-0,75)2 = -1/ 4 +9/16 =5/16 = (5½ /4)2.
Cercle de centre (-0,5 ; 0,75) de rayon 5½ / 4 privé du point A.
d) Le trianle ABC est rectangle isocèle. Vrai.
zB-zA=1-0,5i
AB2 = |zB-zA| 2= 1+0,52 =1,25 = 5 / 4..
zC-zA=0,75 +0,25i
AC2 = |zC-zA| 2= (3 / 4)2+(1 / 4)2 =10 / 16 = 5 / 8.
zC-zB= 0,25 +0,75i
BC2 = |zC-zB| 2= (1 / 4)2+(3 / 4)2 =10 / 16 = 5 / 8.
AC = BC, le triangle est isocèle.
AC2 +BC2 =AB2 ; le triangle est rectangle en C.
|
|