Mathématiques,
Concours EMIA 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. Dérivées, primitives, intégrales..
1- Calculer les dérivées des fonctions suivantes.
f1(x) = exp(x4).
On pose u = x4 ; u' = 4 x3. f '1(u) = u' eu = 4 x3 exp(x4).
f2(x) = exp(x).4
On pose u = ex ; u' = ex ; f 2(u) = u4 ; .f '2(u) =4u'u3.
f '2(x) = 4 exp(x)4.
f3(x) = ln[(x+1) /(x-1)] sur ]1 ; +oo[.
On pose w = (x+1) / (x-1).
puis u = x+1 et v = x-1 ; u' = v' = 1.
w' = (u'v-v'u) / v2 =(x-1-(x+1)] / (x-1)2 = -2/ (x-1)2 .
f '3(x) =w' / w = -2/ ((x-1)(x+1))=-2/(x2-1)..
f4(x) = x sin(ln(x)) sur ]0 ; +oo[.
On pose u = x et v = sin(ln(x)) ; u' = 1 ; v' = cos(ln(x) / x.)
u'v+v'u =sin(ln(x))+cos(ln(x).
2- Calculer les intégrales suivantes :
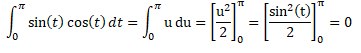
On pose u = sin(t) et du = cos(t)dt.
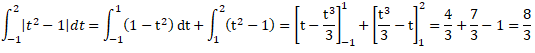
Sur [-1 ; 1], |t2-1| = 1-t2 ; .sur [1 ; 2], |t2-1| = t2 -1.
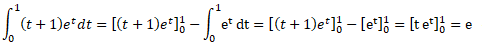
On pose u' = et; v = t+1 ; u =et ; v' = 1 ; intégration par parties.
3-a Soit x un réel positif. Montrer que pour tout t appartenant à [0 ; x], -x2 < t2 cos(t) < x2.
-1 < cos(t) < 1 ; -t2 < t2 cos(t) < t2.
Or t < x ; -x2 < t2 cos(t) < x2.
b. En déduire pour x positif un encadrement de l'intégrale suivante.
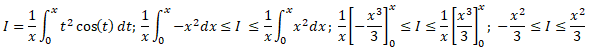
c. Utiliser la question précédente pour déterminer si elle exisste la limite de I en 0+.
-x2 / 3 tend vers 0- ; x2 / 3 tend vers 0+ ; I tend vers zéro.
Exercice 2. Géométrie.
1. Rappeler l'équation d'un cercle C de centre (-1 ; 0) et de rayon 1.
(x-(-1)2 +(y-0)2 = 12 ; (x+1)2 +y2 = 1.
2. Soit (x ; y) un point de C tel que y > 0. Exprimer y en fonction de x.
y = [1- (x+1)2 ]½= [-x(x+2)]½.
3. En déduire dans un repère orthonormé la représentation du graphe de f(x) =[-x(x+2)]½.
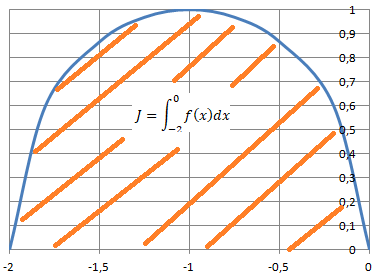
Demi-circonférence.
J représente l'aire du demi disque de rayon 1. J =0,5 p.
Exercice 3- Equation et fonction.
1. Résoudre :
ln(1-x2) -ln(3x) +ln(2)=0.
1-x2 >0 soit -1 < x < 1.
ln[2 (1-x2)/ (3x)] =0 ; 2 (1-x2)/ (3x) = e0 = 1.
1-x2 =1,5x ; x2 +1,5x -1=0
Discriminant D =1,52+4 =6,25=2,52.
Solution retenue : x =(-1,5 +2,5) / 2 =0,5.
ex+e1-x=e+1.
ex+e / ex=e+1 ; e2x +e = (e+1)ex. On pose X = ex >0.
X2+e = (e+1)X ; X2- (e+1)X+e=0.
Discriminant D =(e+1)2-4e =(e-1)2.
Solutions retenues : X =(e+1+e-1)/2=e ; X =(e+1-e+1)/2=1.
e = ex ; x= 1 ; 1 = ex ; x =0.
2a. Etudier la fonction h(x)=x-ln(1+x) sur ]-1 ; +oo[ et démontrer que pour tout réel x > -1, on a ln(1+x) < x.
h'(x) = 1-1 /(1+x) =(1+x-1) / (1+x) = x /(1+x)
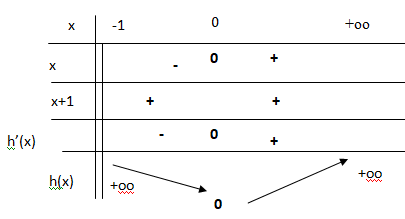
D'après ce tableau, h(x) > 0, donc ln(1+x) < x.
.
b. En déduire que pour tout n entier naturel différent de 0 et 1, on a : (1+1/n)n < e < (1-1/n)-n.
On pose x = 1 /n et on élève à la puissance n :
ln(1+1/n)n < 1/nn ; (1+1/n)n < exp(1/nn)= e1 = e.
- ln(1+x) > -x.
On pose x = -1 /n et on élève à la puissance n :
-ln(1-1/n)n > 1/nn ; ln(1/(1-1/n)n ) > 1/nn ;
1/ (1-1/n)n > exp(1/nn)= e1 = e. (1-1/n)-n > e.
Exercice 4. Etude d'une suite numérique.
On considère la suite (un) définie par u0 = 3 et un+1=(4un-2) / (un+1) pour tout entier naturel n.
On pose f(x) = (4x-2) / (x+1) pour x < 1
1. Etudier les variations de f sur [1 ; +oo[
Calcul de f '(x) en posant u = 4x-2 et v = x+1 ; u' = 4 ; v' = 1.
(u'v-v'u) / v2 =(4x+4-4x+2) / (x+1)2 = 6/ (x+1)2 > 0.
Donc f(x) est strictement croissante de 1 à 4 sur [1 ; +oo[ et décroissante sur [0 ; 1].
2. Démontrer que pour tout n > 0, on a un > 1.
un+1=f(un) > 1.
3. On définit la suite (vn) en posant : vn =(un-2) / (un-1) pour tout entier naturel. Démontrer que (vn) est géométrique et donner l'expression de son terme général.
vn+1 = (un+1-2) / (un+1-1) ; un+1-2 =(4un-2) / (un+1) -2 = (2un-4) / (un+1) ; un+1-1 =(4un-2) / (un+1) -1 = (3un-3) / (un+1).
vn+1 = (2un-4) / (3un-3) =2 / 3 (un-2) / (un-1)=2 / 3 vn.
La suite (vn) est géométrique de raison 2 /3 et de premier terme v0 =(3-2) /(3-1) =0,5.
vn =0,5 *(2/3)n.
4. En déduire l'expression du terme général de la suite (un).
un-2=0,5 *(2/3)n.(un-1) ; un-0,5 *(2/3)n un =2-0,5 *(2/3)n.
un =2-0,5 *(2/3)n / (1-0,5 *(2/3)n).
5. Justifier que (un) est convergente et déterminer sa limite.
un+1-un=f(un)-un ; (4x-2) / (x+1)-x =(3x-3) / (x+1) < 0 sur [0 ; 1] ; la suite est décroissante.
Quand n tend vers l'infini, (2/3)n tend vers zéro et un tend vers 2.
La suite est décroissante et bornée, donc elle converge.
Exercice 6. Calculs algébriques.
On s'intéresse à l'égalité n°1 : 1 / a +1 /b = 1 /(a+b) qui est fausse en général.
1. Donner un contre exemple à cette égalité.
Pour a = 1 et b = 2, l'égalité est fausse.
2.a. a et b sont des nombres complexes non nuls. Démontrer que cette égalité est vraie si et seulement si a2+b2+ab = 0.
a = c+i d et b = e + i f avec c, d, e et f réels.
Si 1 / a +1 /b = 1 /(a+b)
alors : 1 /a + 1 /b =(a+b) / ab = 1 /(a+b) ; (a+b)2 = ab ; a2+b2+2ab = ab ; a2+b2+ab = 0.
Si a2+b2+ab = 0 alors : a2+b2+2ab - ab =0 ; (a+b)2 = ab ; (a+b) / ab = 1 /(a+b) ; 1 / a +1 /b = 1 /(a+b).
b. Un cas particulier ; déterminer les nombres complexes z1 et z2 tels que l'égalité 1 soit vraie pour b = 2 et a = z1 ou a = z2.
a2+4+2a = 0 ; (a+2)2 = 0 ; a = -2.
c. On revient au
cas général. En posant z = a / b, montrer que 1 se ramène à une
équation de degré 2 en la variable z dont on donnera l'expression des
solutions sous forme exponentielle.
a = z b ; (zb)2 +b2 +zb2=0 ; z2+z+1=0.
Discriminant : D =1-4 = -3 = 3 i2 .
z1 =(-1 +3½i) / 2 = cos (-4p/6 )+ i sin (-4p/6)= exp( -4 i p/6).
z2 =(-1 -3½i) / 2 = cos (7p/6 )+ i sin (7p/6)= exp( i 7p/6).
|
...
|
....
|
Exercice 7 : Polynômes.
1.
Soit P(X) = aX3+bX2+cX+d avec a, b, c et d réels et a non nul. On
suppose que P possède trois racines réelles. Exprimer la somme de ces
trois racines en fonction de a, b, c et d.
P(X) = a(X-x1)(X-x2)(X-x3).
P(X) =[aX2-a(x1+x2)X+ax1x2)](X-x3)=aX3-a(x1+x2)X2+ax1x2X-ax3X2+a(x1+x2)x3X-ax1x2x3.
On identifie : b=-a(x1+x2+x3) ; x1+x2+x3= -b / a.
a(x1+x2)x3+ax1x2= c ; -ax1x2x3 = d.
2. Appliquer l'algorithme d'Euclide aux polynômes P et Q suivants : P(X) = X2-4X+4 et Q(X) = X2+3X-10.
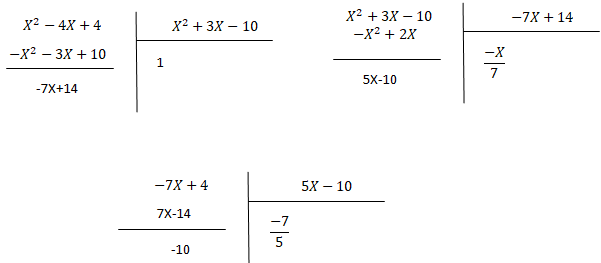
Exercice 9 . Trigonométrie.
A = sin (p/14) sin(3p/14) sin(5p/14)
1. Rappeller les formules donnant cos(a+b) et sin(a+b).
cos(a+b)= cos(a) cos(b) -sin(a) sin(b).
sin(a+b)=sin(a) cos(b) + sin(b) cos(a).
2. En déduire que sin(a) cos(b) = 0,5( sin(a+b) +sin(a-b)) et sin(a) sin(b) = 0,5(cos(a-b) -cos(a+b)).
sin(a+b)=sin(a) cos(b) + sin(b) cos(a).
sin(a-b)=sin(a) cos(b) - sin(b) cos(a).
Ajouter : 2sin(a) cos(b) =sin(a+b) +sin(a-b).
sin(a) cos(b) = 0,5( sin(a+b) +sin(a-b)).
cos(a-b)= cos(a) cos(b) +sin(a) sin(b).
cos(a+b)= cos(a) cos(b) -sin(a) sin(b).
Soustraire : 2sin(a) sin(b) = cos(a-b) -cos(a+b).
sin(a) sin(b) = 0,5(cos(a-b) -cos(a+b)).
3. Montrer que A cos (p/14) = 1 /8[sin(3p/7) +sin(2p/7)-sin(5p/7)].
A cos (p/14) = sin (p/14)cos (p/14) sin(3p/14) sin(5p/14).
sin (p/14)cos (p/14)= 0,5sin(p/7).
0,5sin(p/7) sin(3p/14) =0,25(cos(p/14) -cos(5p/14)).
0,25(cos(p/14) -cos(5p/14))sin(5p/14) = 0,25[cos(p/14)sin(5p/14) -cos(5p/14)sin(5p/14)]
.cos(p/14)sin(5p/14) =0,5( sin(3p/7) +sin(2p/7)).
cos(5p/14)sin(5p/14) =0,5( sin(5p/7).
A cos (p/14) =0,125( sin(3p/7) +sin(2p/7)-sin(5p/7)).
4. Montrer que A = 1/8.
sin(5p/7) =sin(p-2p/7) ; sin(2p/7)=sin(p-2p/7) ; sin(3p/7) = cos (p/2-3p/7).
sin(3p/7) +sin(2p/7)-sin(5p/7)=cos (p/2-3p/7)+sin(p-2p/7)-sin(p-2p/7)= cos (p/2-3p/7)=sin(3p/7)=sin(6p/14) =cos (p/14) .
|
|