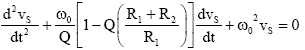|
Etude d'un filtre de Wien. concours Mines 06 sans calculatrice. En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
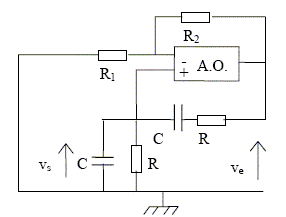
Soit le filtre ci-dessous où les résistances R sont identiques, ainsi que les capacités C des condensateurs.
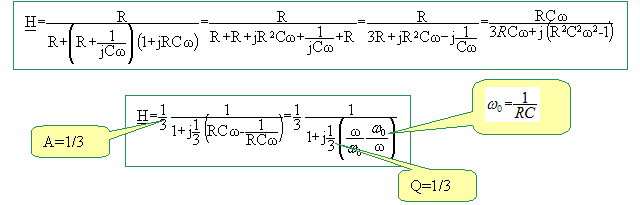
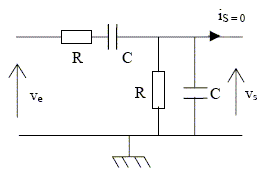
Filtre en régime sinusoïdal permanent. Le filtre est alimenté par une tension d’entrée ve = Ve cos(wt). A la sortie, on a alors une tension vs = Vs cos(wt + j ). Il n’y a pas de charge à la sortie. On associe à ces tensions les grandeurs complexes : ve = Ve exp(jwt) et vs = Vs exp(jwt) avec Vs =Vs exp(jj). Etablir la fonction de transfert
sous la forme :
Admittance complexe des branches en dérivation : Y= 1/R + jCw = (1+RCw )/R Impédance complexe correspondante : Z1=R/(1+RCw) Impédance complexe de l'ensemble : Z = R+1/(jCw) + R/(1+RCw) H= vs /ve = Z1 / Z.
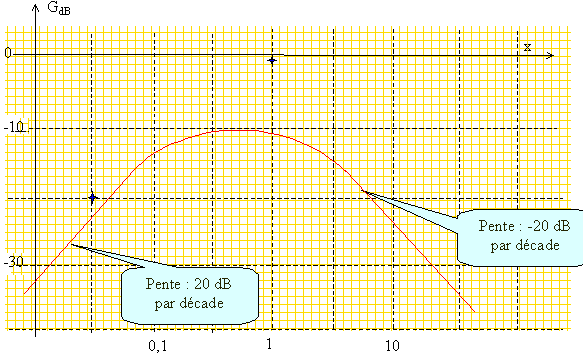
GdB = 20 log |H|
Quand x tend vers l'infini, GdB est équivalent à : 20 ln A - 10 ln (Qx)2 soit -20 ln(Qx)=-20 log (x/3). Quand x=1, GdB =20 ln A= 20 ln(1/3) = -20 ln3 = -10.
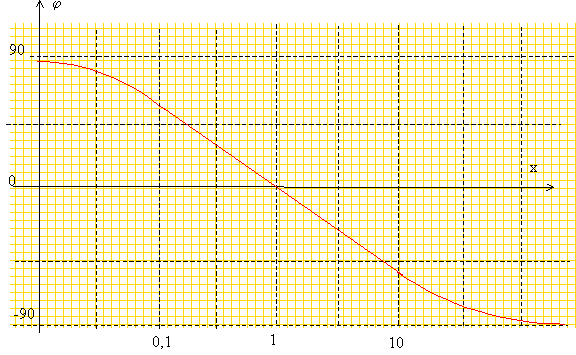
si x tend versl'infini, tan j est équivalent à -x/9. Si x=1, tan j = 0
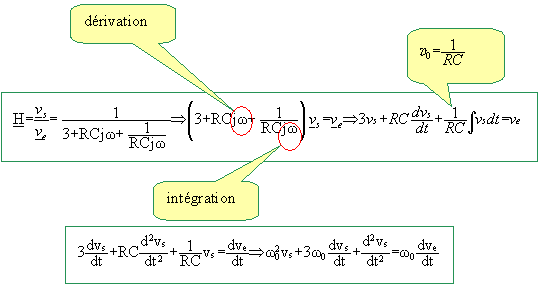
Le filtre est à présent alimenté par une tension d’entrée quelconque, dont la valeur instantanée est ve(t). Etablir l’équation différentielle liant vs(t) et ve(t) : on pourra pour cela utiliser la fonction de transfert.
Oscillateur quasi-sinusoïdal : Le filtre de Wien est couplé à un amplificateur opérationnel (A.O.) parfait, dont le fonctionnement est supposé linéaire : voir schéma ci-dessous.
Aucun générateur n’est présent dans ce circuit. Qu’appelle t-on amplificateur opérationnel ‘parfait’ (ou idéal) ? Les intensités des courants d'entrées sont nulles et la tension e= V+-V- =0. Que signifie l'expression ‘fonctionnement linéaire’ ? La tension de sortie est proportionnelle à la tension d'entrée. Le coefficient de proportionnalité dépend de R1, R2.
Etablir la relation reliant V-, potentiel à l’entrée inverseuse de l’A.O, et Ve en fonction de R1 et R2. En appliquant le théorème de Millmann : V- =[ Ve/R2 ] / [1/R1+1/R2] ; V- = R1 Ve/(R1+R2) ; V- =Vs = R1 Ve/(R1+R2). (1) En déduire que l’équation différentielle suivie par vs(t) est : (1) donne : dve/dt = (R1+R2) / R1 dvs/dt. repport dans : w02vs + 3w0dvs/dt +d2vs/dt2 = w0dve/dt avec Q=1/3. d'où : d2vs/dt2 + w0/Q [ 1-Q(R1+R2) / R1]dvs/dt+ w02vs=0. A quelle condition la solution de cette équation est-elle purement sinusoïdale ? 1-Q(R1+R2) / R1 =0 soit 3 R1 = R1+R2 ; 2 R1 =R2. Que se passe-t-il si le terme 1-Q(R1+R2) / R1 est strictement négatif ? Quel est alors le mode de fonctionnement de l’amplificateur opérationnel ? vs va atteindre rapidement la valeur de la tension de saturation de l'A.O. Ce dernier fonctionnera alors en régime de saturation.
|
|||||||
|
|
|||||||
|
|
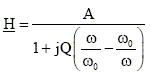en
précisant les valeurs de A, de Q et l’expression
de w0
en fonction de R et
C.
