|
QCM : dipole RL, RLC, oscillateurs mécaniques, photon : concours kiné Poitiers 1999.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
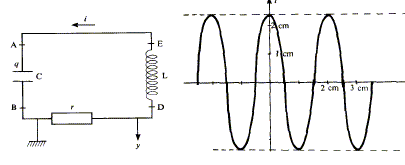
On néglige l'énergie dissipée dans le circuit. On prendra pi2 = 10. Sur l'écran de l'oscilloscope on observe i(t) avec un balayage horizontal de 25 µs / cm et une sensibilité de déviation verticale de 2 mA / cm, on observe la courbe représentée ci-dessous :
La capacité du condensateur est : 2,5 nF ; 2,5 µF. Une période T correspond à 2 cm soit 2*25 = 50 µs = 5 10-5 s. T =2 pi (LC)½ ; T2 = 4 pi2 LC ; C = T2 /( 4 pi2 L )=(5 10-5)2 / (40*0,025) =25 10-10 F = 2,5 10-9 F = 2,5 nF. L'énergie électrique emmagasinée dans le circuit est : 0,3 J ; 0,3 µJ ; 0,3 mJ. Lorsque l'intensité est maximale la bobine inductive stocke toute l'énergie. imax correspond à 2,5 cm soit 2,5*2 = 5 mA = 5 10-3 A. Energie stockée dans l'inductance : ½L i2max=0,5 * 0,025*(5 10-3)2=3,1 10-7 J = 0,3 10-6 J = 0,3 µJ.
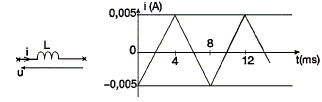
Une bobine longue de 1000 spires, d'inductance L = 5 mH et de résistance négligeable est parcourue par un courant i variable dans le temps représenté sur la figure suivante :
La tension aux bornes de la bobine est : t appartient [0 ; 4 ms] ; u = 2,5 V ; t appartient [0 ; 4 ms] ; u = 12,5 V ; t appartient [0 ; 4 ms] ; u = 12,5 mV ; t appartient [4 ms ; 8 ms] ; u = -12,5 mV ; t appartient [4 ms ; 8 ms] ; u = -12,5V. u = L di/dt ; entre 0 et 4 ms l'intensité est croissante : di /dt = +0,010 / 4 10-3 = 2,5 A s-1 u = 5 10-3*2,5 =12,5 10-3 V = 12,5 mV. entre 0 et 4 ms l'intensité est décroissante : di /dt = -0,010 / 4 10-3 = -2,5 A s-1 u = -5 10-3*2,5 =-12,5 10-3 V = -12,5 mV.
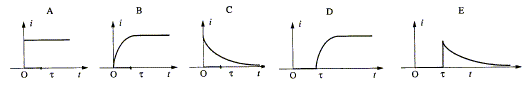
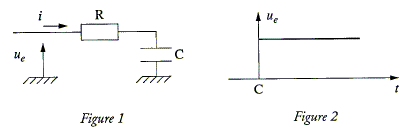
Lors de la charge d'un condensateur à travers une résistance, l'intensité décroît de manière exponentielle jusqu'à s'annuler en fin de charge. L'intensité est maximale à t = 0. Graphe C.
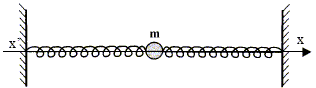
Soit un ressort de raideur k et de masse négligeable à l'extrémité duquel on accroche une masse m. On écarte la masse de sa position d'équilibre en tirant sur le ressort d'une faible distance a et on lâche la masse m à un instant pris comme origine des dates. Laquelle des deux propositions suivantes est exacte ? - L'équation différentielle du mouvement de m est : d2x/dt2 + km x = 0 ( d2x / dt2 + k / m x = 0 ) - L'équation horaire du mouvement est du type x = a sin ( 2 pi t / T + j ) où T est la période de l'oscillateur et j une constante qui dépend des conditions initiales. ( Vrai ) On place maintenant la masse m entre deux ressorts identiques de raideur k et de masse négligeable. On tire sur les deux extrémités de l'ensemble qu'on accroche à des potences fixes. On écarte légèrement la masse m de sa position d'équilibre suivant l'axe x'x et on la lâche à l'instant t=0.
Laquelle des trois propositions suivantes est exacte ? - L'équation différentielle du mouvement est d2x/dt2 + 2k / m x = 0. ( Vrai ). - L'équation différentielle du mouvement est d2x/dt2 + k /(2 m) x = 0. - L'équation différentielle du mouvement est d2x/dt2 + 2k m x = 0.
Laquelle des trois propositions suivantes est exacte ? - Les deux pendules oscillent avec la même période ( Vrai : la période est indépendante de la masse T = 2 pi (L / g)½ ). - Le pendule de masse m' = 4 m oscille avec une période deux fois plus grande que celui de masse m. - Le pendule de masse m' = 4 m oscille avec une période deux fois plus faible que celui de masse m. On utilise maintenant deux pendules simples de même masse mais de longueurs différentes L' = 4 L. Laquelle des deux propositions suivantes est exacte ? - Les deux pendules oscillent avec la même période. - Le pendule de longueur L' = 4 L oscille avec une période deux fois plus grande que celui de longueur L.( Vrai : la période est indépendante de la masse T = 2 pi (L / g)½ ).
Une radiation monochromatique rouge a une longueur d'onde dans le vide l0 = 750 nm. c = 3 108 m/s. Parmi les propositions suivantes lesquelles sont exactes ? - La fréquence de cette radiation est : n = 4 1014 Hz. ( Vrai ). n = c / l0 =3 108 / 750 10-9 = 4 1014 Hz. - Dans l'air l'oeil humain est sensible aux ondes électromagnétiques dont les longueur d'ondes sont comprises entre 400 et 750 nm environ. ( Vrai ).
- Les radiations infra-rouges ont des longueurs d'onde inférieures à celles des rayons UV. l infra-rouges > l UV. - Les photons associés à des rayons X de longueur d'onde l = 0,2 nm sont plus énergétiques que les photons associés à des ondes infra-rouge. ( Vrai ). - Dans l'eau la longueur d'onde de la radiation monochromatique rouge est toujours 750 nm. La longueur d'onde dépend du milieu de propagation.
|
|||||||
|
|
|||||||
|
|