Mathématiques,
probabilités
Bac Sti2d et Stl 2015.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Nlle Calédonie.
1.
Dans une usine, une machine remplit automatiquement avec de l’huile de
moteur des bidons pouvant contenir au maximum 102 litres. Pour pouvoir
être commercialisé, un bidon doit contenir au
moins 98 litres
d’huile. La quantité d’huile, exprimée en litres, fournie par la
machine peut être modélisée par une variable aléatoire X qui suit une
loi normale d’espérance µ = 100 et d’écart-type s = 0,8.
a. Déterminer la probabilité de
l’évènement « X > 102 » et interpréter ce résultat.
(102-µ) / s
=2/0,8 = 2,5. P(t=2,5)
=0,9938.
p(X <=102) = 0,9938 ; P(X >102) =
1-0,9938 =0,0062.
C'est la probabilité pour que le bidon déborde lors du remplisage.
b. Déterminer le pourcentage de
bidons qui ne pourront pas être commercialisés en expliquant
votre démarche.
Bidons pouvant être commercialisés :
Loi normale centréevréduite :v(98-100) / 0,8 = -2,5. P(2,5) = 0,9938.
1-0,9938 = 0,0062.
0,62 %des bidons ne peuvent pas être commercialisés.
2. On estime que 99,4% des bidons
sont remplis correctement.
Soit Y la variable aléatoire qui, à chaque lot de 30 bidons prélevés au
hasard dans la production de
l’usine,
associe le nombre de bidons non correctement remplis. Le stock est
suffisamment important pour que ce prélèvement soit assimilé à un
tirage avec remise.
Après avoir précisé la loi suivie par Y ,
calculer la probabilité qu’il y ait au plus un bidon
non correctement rempli dans un lot de 30 bidons.
Loi binomiale n =30 ; p = 0,006 ; q = 1-p = 0,994.
P(Y=0) =C030 q30 p0 =
0,99430 =0,8348.
P(Y=1) =C130 q29 p1 =
30*0,99429 *0,006=0,1512.
P(Y=0) +P(Y=1) =0,8348 +0,112 = 0,986.
|
|
|
Métropole septembre
Un
sismologue déclare en janvier 2014 : « Le risque d’un séisme majeur le
long de la faille de San Andreas, en Californie, dans les vingt
prochaines années est supérieur à 70%».
On s’intéresse au temps,
exprimé en années, écoulé entre deux séismes majeurs le long de cette
faille en Californie. On admet que ce temps est une variable aléatoire
X qui suit une loi exponentielle de paramètre l.
1. Pour illustrer
la situation un élève utilise un tableur.
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
| Année |
1769 |
1800 |
1808 |
1857 |
1865 |
1868 |
1906 |
1925 |
1927 |
1938 |
1952 |
1957 |
1971 |
1989 |
2004 |
2008 |
2010 |
2011 |
Total |
|
|
31 |
8 |
49 |
8 |
3 |
38 |
19 |
2 |
6 |
19 |
5 |
14 |
18 |
15 |
4 |
2 |
4 |
245 |
a.
Proposer un titre pour la cellule A2 grisée.
Durée ( en années) séparant deux séismes consécutifs de magnitude
supérieure à 5.
b. Quelle
formule a saisi l’élève dans la cellule C2 afin de compléter ce tableau
jusqu’à la colonne S par « recopie automatique vers la droite » ?
=C$1-B$1.
2. a. Calculer en
années la moyenne m, arrondie à 10−2 près, du temps écoulé
entre deux séismes majeurs le long de la faille de San Andreas en
Californie.
18 séismes majeurs entre 1769 et 2011 soit 17 intervalles de temps
entre deux séismes.
245 / 17 =14,41 ans.
b. Justifier qu’une
approximation du paramètre l¸
de la loi exponentielle suivie par la variable aléatoire X est 0,069 4.
1 / 14,41 = 0,0694 an-1.
3. a. Calculer P(X
<20) à 10−2 près.
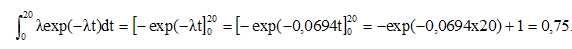
b. L’affirmation du
sismologue paraît-elle cohérente avec cette modélisation par une loi
exponentielle ?
L'affirmation est cohérente, 0,75 est proche de "supérieure à 70 %".
4.
Le dernier séisme majeur a eu lieu en 2014 à Napa. Calculer la
probabilité qu’il n’y ait pas d’autres séismes majeurs le long de la
faille de San Andreas, en Californie, avant 2050. On arrondira à 10−2
près.
2050-2014 =36 ; P(X >36) = 1-P(X <=36).
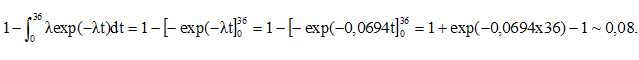
5. a. Résoudre
l’équation 1−exp(−0,0694t) = 0,95. Interpréter ce résultat.
exp(−0,0694t)
=0,05 ; -0,0694 t = ln 0,05 ; t = 43,17.
La probabilité qu'il y ait un séisme majeur dans les 43 prochaines
années est supérieure à 95 %.
.
|
|
|
|
Antilles Guyanne.
L’entreprise
BUENPLATO produit en grande quantité des plats préparés sous vide.
L’objectif de cet exercice est d’analyser la qualité de cette
production en exploitant divers outils mathématiques.
1. Sur
les emballages, il est précisé que la masse des plats préparés est de
400 grammes. Un plat est conforme lorsque sa masse, exprimée en gramme,
est supérieure à 394 grammes. On note M la variable aléatoire qui, à
chaque plat prélevé au hasard dans la production, associe sa masse en
gramme. On suppose que la variable aléatoire M suit la loi normale
d’espérance 400 et d’écart type 5.
a. Déterminer la
probabilité qu’un plat prélevé au hasard ait une masse comprise entre
394 et 404 grammes.
Probabilité que la masse soit inférieure à 394 g :
(394-400) / 5 = -1,2 ; P(1,2)
=0,8849 ; P(-1,2)
=1-0,8849 = 0,1151.
Probabilité que la masse soit supérieure à 404 g.
(404-400) / 5 = 0,8 ; P(0,8)
=0,7881 ; 1-0,7881
= 0,2119.
Probabilité que la masse soit comprise entre 394 et 404 g :
1-0,1151-0,2119 =0,673.
b. Déterminer la
probabilité qu’un plat soit conforme.
1-0,1151 = 0,8849 ~0,885.
2.
Les plats préparés sont livrés à un supermarché par lot de 300. On
arrondit la probabilité de l’évènement « un plat préparé prélevé au
hasard
dans la production n’est pas conforme » à 0,12. On prélève au
hasard 300 plats dans la production. La production est assez importante
pour que lion puisse assimiler ce prélèvement à un tirage aléatoire
avec remise.
On considère la variable aléatoire X qui, à un lot de
300 plats, associe le nombre de plats préparés non conformes qu’il
contient.
a. Justifier que
la variable aléatoire X suit une loi binomiale dont on précisera les
paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 300. La
probabilité qu'un plat soit non conforme est constante p = 0,12. La
probabilité qu'un plat soit conforme est q =1-p =0,88.
X
suit la loi binomiale de paramètre n = 300 et p = 0,12.
b. Calculer
l’espérance mathématique E(X) et en donner une interprétation.
E(X) = np = 300 x 0,12 = 36.
En moyenne, il y a 36 plats non conformes sur 300 plats.
c. Calculer la
probabilité que dans un échantillon de 300 plats prélevés au hasard, au
moins 280 plats soient conformes.
Il y a au plus 20 plats non conformes. La calculatrice donne P(X
<=20) ~0,002.
3.
Le fabricant annonce sur les étiquettes de ses produits une proportion
de produits non conformes de 12%. On prélève au hasard dans la
production un échantillon de taille 1 200 dans lequel 150 plats se
révèlent être non conformes.
a. Quelle est la
fréquence de plats non conformes dans l’échantillon prélevé ?
f = 150 / 1200 = 0,125.
b.
Déterminer l’intervalle de fluctuation avec un niveau de confiance de
95% de la fréquence de plats non conformes dans un échantillon de
taille 1200.
Ecart type s=( pq
/ n)½ =(0,125 *0,875 / 1200)½ =9,55 10-3
; 1,96 s=1,96 x
9,55 10-3 ~0,019.
Intervalle de fluctuation [ 0,125-0,019 ; 0,125 +0,019 ] soit [0,106 ; 0,144 ].
c. L’échantillon
est-il représentatif de la production du fabricant ? Justifier.
0,12 appartient à cet intervalle : l'échantillon est représentatif de
la production.
|
|
Métropole.
L’usine
OCEFRAIS embouteille des jus de fruits. L’étiquette de la bouteille
indique 1,5 litre de jus de fruits. Le volume de la bouteille est de 1,
55 litre. À l’embouteillage, le volume de jus de fruits versé dans une
bouteille est une variable aléatoire X qui suit la loi normale de
moyenne µ = 1,5 et d’écart-type ¾
= 0,015.
1. a. L’une des
trois figures donne la courbe représentative Cf de la
densité f de cette loi normale. Indiquer sur la copie le numéro de la
figure correspondante en expliquant votre choix.
La courbe 3 est centrée sur la
moyenne et symétrique par rapport à la droite d'équation x = 1,5.
b. Déterminer
P(1,485<= X <=1,515).
(1,485-1,5) / 0,015 = -1 ; (1,515-1,5) / 0,015 = +1 ; P(1) = 0,8413 : 2P(1)
-1 = 2 x0,8413-1 = 0,6826 ~0,683.
2.
On choisit au hasard une bouteille de jus de fruits.
a. Quelle est la
probabilité que cette bouteille contienne exactement 1,48 litre de jus
de fruits ?
Cette probabilité est nulle :
la loi normale n'est pas une loi discrète.
b. Calculer la
probabilité que cette bouteille contienne entre 1,46 litre et 1,54
litre de jus de fruits.
(1,46-1,5) / 0,015 =
-2,667 ; (1,54-1,5) / 0,015 = +2,667 ; P(2,667) = 0,9662 : 2P(1)
-1 = 2 x0,9962-1 ~0,992.
c.
Quelle est la probabilité que cette bouteille déborde sur la chaîne
d’embouteillage
1-p(X <= 1,55) ; (1,55-1,5) / 0,015 =3,333 ; P(3,333)
= 0,9996 ; 1-0,9996 ~0,0004.
3.
Une bouteille est dite conforme si elle contient entre 1,46 litre et
1,54 litre de jus de fruits. Selon l’usine OCEFRAIS, la probabilité
qu’une bouteille soit non conforme est 0,007 7. Un supermarché achète
un lot de 10 000 bouteilles.
a. Déterminer
l’intervalle de fluctuation asymptotique à 95%de la fréquence observée
de bouteilles non conformes dans un tel lot.
p = 0,0077 ; q = 1-p = 0,9923 ; n = 10 000 ; (pq / n)½ =
(0,0077 x 0,9923 / 10000)½ =8,74 10-4. ; 8,74 10-4x 1,96 = 0,00171.
Intervalle de fluctuation : [0,0077 -0,00171 ; 0,0077 +0,00171 ] soit [0,0060 ; 0,0094 ]
b.
Dans le lot de 10 000 bouteilles, on a compté 90 bouteilles non
conformes. Le gérant du supermarché trouve le nombre de bouteilles non
conformes anormalement élevé.
L’usine OCEFRAIS a-t-elle des raisons de s’inquiéter ?
90 / 10000 =0,0009. Cette valeur appartient à l'intervalle de
fluctuation. L'usine n'a pas à s'inquiéter.
Polynésie.
Une entreprise achète du sucre et le revend après conditionnement à des
grossistespour le marché de la grande distribution.
1.
Une machine de l’usine conditionne des paquets de sucre en poudre de 1
kg. La masse M en gramme d’un paquet est une variable aléatoire qui
suit la loi normale de moyenne m = 1000 et d’écart-type s = 7.
a. Calculer
P(995<= X <=1005).
(995-1000) / 7 ~ 0,714 ; 10005-1000) / 7 ~0,714 ; P(0,714) =0,7622 ;
2 P(0,714) -1 = 2 x 0,7622-1 =0,524.
b. Un
paquet est refusé si sa masse est inférieure à 990 grammes. Quelle est
la probabilité pour qu’un paquet conditionné par cette machine soit
refusé ?
(990-1000) / 7 ~-1,43 ; P(1,4286) =0,922 ; 1-0,922 ~0,078.
Dans
la suite de l’exercice, on arrondit à 0,08 la probabilité p pour qu’un
paquet conditionné dans l’usine soit refusé, ainsi p = 0,08. On
s’intéresse au stock journalier de paquets conditionnés dans l’usine.
2.
On prélève au hasard 100 paquets parmi le stock. Le stock est
suffisamment important pour que l’on puisse assimiler ce prélèvement à
un tirage aléatoire avec remise.
On note X la variable aléatoire égale au nombre de paquets à rejeter
dans cet échantillon.
a. Quelle est la
loi de probabilité de X ? On donnera ses paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 100. La
probabilité qu'un paquet soit non conforme est constante p = 0,08. La
probabilité qu'un paquet soit conforme est q =1-p =0,92. X
suit la loi binomiale de paramètre n = 100 et p = 0,08.
b. Quelle est la
probabilité qu’exactement 3 paquets parmi ces 100 paquets soient
refusés ?
p(X =3) = C1003 q97 p3 =100
x 99 x 98 / 6 x 0,9297 x 0,083 = 0,0254 ~0,025.
c. Calculer la
probabilité que, parmi ces 100 paquets, 5 ou plus soient refusés.
p(X=0) = C1000 q100 p0 =1 x
0,92100 x 1 = 2,4 10-4.
p(X=1) = C1001 q99 p1 =100
x 0,9299 x 0,08 = 0,00208.
p(X=2) = C1002 q98 p2 =100
x99 / 2x 0,9298 x 0,082 = 0,00895.
p(X=4) = C1004 q96 p4 =100
x99 x98 x97 / (2x3 x4) x 0,9296 x 0,084 = 0,05363.
1-p(X<5)=1-(2,4 10-4+ 0,00208 +0,0895 +0,0254 +0,05363 ) =0,83.
3.
On contrôle la masse d’un échantillon de 100 paquets de sucre dans le
stock global de l’entreprise. Après contrôle, 10 paquets sont refusés.
L’échantillon est-il représentatif de la production de l’usine ?
Justifier.
Ecart type s =
(pq /n)½ =(0,08 x0,92 / 100) ½ =0,027 ; 1,96 x
0,027 = 0,053.
Intervalle de fluctuation asymptotique à 95 % : [ 0,08-0,053; 0,08
+0,053 ] soit [0,027 ; 0,133 ].
10
/100 = 0,10 , cette valeur appartient à l'intervalle de fluctuation ;
l'échantillon est représentatif de la production. |
|