QCM mathématiques.
Concours Advance 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
1. Soit la fonction numérique définie sur R-{1} par f(x) =(x+3) / (x+1).
A. f est continue sur ]-oo ; -1 [. Vrai.
B. Pour tout x appartenant à R-{-1}, f '(x) = 2 / (x+1)2. Faux.
On pose u = x+3 et v = x+1 ; u' =1 ; v' = 1.
(u'v -v'u) / v2 = ( x+1-x-3) / (x+1)2 = -2 /(x+1)2.
C. La limite de f(x) est égale à 1 lorsque x tend vers l'infini. Vrai.
D. f est décroissante sur ]-1 : +oo[.
Vrai.
f '(x) est négative ; f(x) est décroissante sur son intervalle de définition.
E. L'équation f(x) =0 admet une unique solution sur l'intervalle de définition. Vrai.
x = -3.
2.
Soient deux fonctions définies sur R par f(x) = 1-4ex / (e2x+1) et g(x) = e2x-1.
A. Pour tout x appartenant à ]-oo ; 0], g(x) est négatif ou nul. Vrai.
1 / e-2x est inférieur ou égal à 1 sur ]-oo ; 0].
B. Pour tout x appartenant à [0 ; +oo[, f '(x) est positif ou nul. Vrai.
On pose u = ex et v = e2x+1 ;u' = ex ; v' = 2e2x.
(u'v -v'u) / v2 = (ex(e2x+1) - 2exe2x ) / (e2x+1)2 = ex (1-e2x) / (e2x+1)2
f '(x) = 4ex (e2x-1) / (e2x+1)2 .
C. f(x) est décroissante sur ]-oo ; 0]. Vrai.
La dérivée f '(x) est du signe de e2x-1.
1 / e-2x est inférieur ou égal à 1 sur ]-oo ; 0] ;
f '(x) est donc négative et f(x) est décroissante sur ]-oo ; 0].
D. La limite de f(x) est égale à 1 lorsque x tend vers moins l'infini. Vrai .
Au voisinage de moins l'infini, le terme en exponentielle tend vers zéro.
E. La limite de f(x) est égale à 1 lorsque x tend vers plus l'infini. Vrai .
Par croissance comparée ex / (e2x+1) tend vers zéro lorsque x tend vers l'infini.
3. Soit pour tout x réel, f(x) = 1-cos(2x) et g(x) = sin2(x).
A. f (p/2)=2. Vrai.
f (p/2)=1-cos p = 1-(-1) = 2.
B. Pour tout x réel, f '(x) = sin(2x). Faux.
f '(x) = -(-2) sin (2x) = 2 sin (2x).
C. Pour tout x réel, f '(x) = 2 g'(x). Vrai.
g'(x) = 2 sinx cosx = sin(2x).
D. La limite de g(x) / x2 est égale à 1 quand x tend vers zéro. Vrai.
g(x) / x2 = c La limite de sin(x) / x est égale à 1 quand x tend vers zéro.
E. La limite de f(x) / x2 est égale à 2 quand x tend vers zéro. Vrai.
f(x) = 1-cos(2x) =2sin2(x) ; f(x) / x2 = 2 f(x) / x2 .
|
| .
. |
|
|
4. Soit f la fonction numérique définie sur [1 ; +oo[ par f(x) = ln(2x) +1-x.
A. f(1) >0. Vrai.
f(1) = ln(2)+1-1 = ln(2).
B. Pour tout x appartenant à [1 ; +oo[, f '(x) = (1-x) / x. Vrai.
f '(x) = 2 /(2x) -1 = (1-x) / x.
C. f(x) est strictement décroissante sur [1 ; +oo [. Vrai.
f '(x) est négative sur ]1 ;+ oo [ ; f (x) est strictement décroissante sur ]1 ;+ oo [
D. La limite de f(x) est égale à -oo quand x tend vers plus l'infini. Vrai.
Par croissance comparée, x croît plus vite que ln(2x) quand x tend vers l'infini.
E. Il existe un unique réel a appartenant à [1 ; +oo [, a = ln(2a) +1. Vrai.
5. Soit f une fonction deux fois dérivable sur [-2 ; 3 ] telle que f(0)=1 et dont la dérivée f ' a pour tableau de variation :
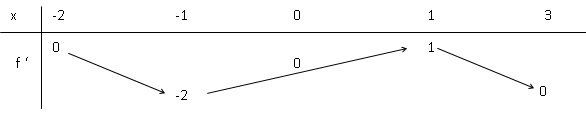
A. f est croissante sur [-1 ; 0]. Faux.
f ' est négative sur [-1 ; 0 ], f est décroissante sur cet intervalle.
B. f est croissante sur [1 ; 3]. Vrai.
f ' est positive sur [1 ; 3 ], f est croissante sur cet intervalle.
De plus f est minorée par f(0)=1.
C. Pour tout x appartenant à [0 ; 3 ], f(x) est supérieure ou égale à 1. Vrai.
f ' est positive sur [0 ; 3] , alors f est strictement croissante sur cet intervalle.
De plus f est minorée par f(0)=1.
D. Pour tout x et x' tels que -2 < x < x' <0, f(x') < f(x). Vrai.
f ' est négative sur ]-2 ; 0 [, alors f est strictement décroissante sur cet intervalle.
E. f(-2) supérieure ou égale à 1. Vrai.
f est strictement décroissante sur ]-2 ; 0 [ et f est minorée par f(0) = 1.
6 . Soit a, b, c,et d quatre entiers naturels non nuls. On a :
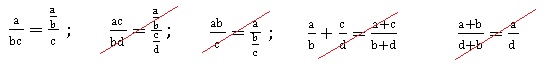
7. Soit D = ]0 ; 1 [ union ]1 ; +oo [ et f définie sur D par f(x) = 1 / [(xln(x)]
A. f est continue sur ]0 ; 1 [. Vrai.
B. La limite de f est égale à plus l'infini quand x tend vers 0+. Faux.
Au voisinage de 0+, ln(x) est négative.
C. Sur ]1 ; + oo [, une primitive F de f est : F(x) = -1 / ln2(x). Faux.
dériver F(x) : on pose u = ln(x) ; u' =1 /x.
F= -1 /u2 = -u-2 ; F ' = -(-2)(1/x) / u3 = 2 / (x ln3(x)).
D. f admet une primitive sur ]0 ; 1 [. Vrai.
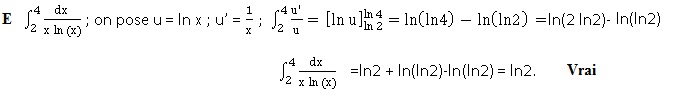
8. Soit f la fonction définie sur [-p ; +p] par f(x) =0,5(p+x) sur [-p ; 0[ et f(x) =0,5(p-x) sur [0 ; p ] .
A. f(x) est continue sur [-p ; +p] . Vrai.
B. f est dérivable sur [-p ; +p] . Faux.
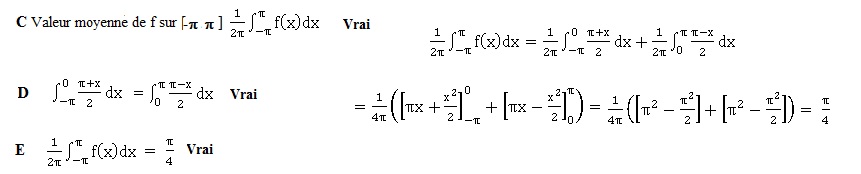
|
|
|
|
9.
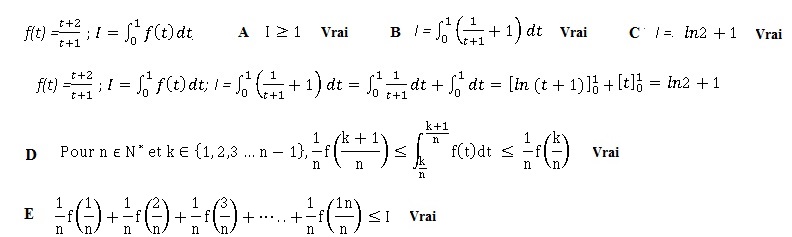 . .
10. Soit z et z' deux nombres complexes.
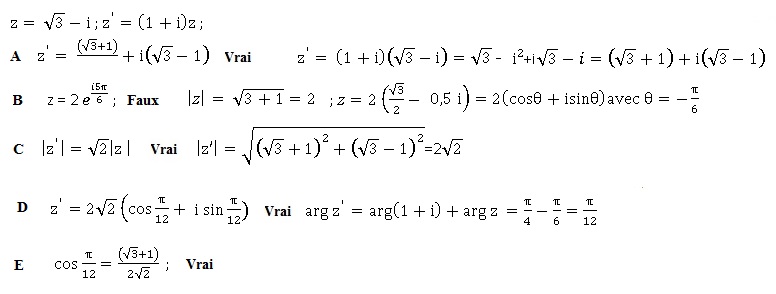
11. Dans
l'espace muni d'un repère orthonormé, on considère les points P(3 ; -1
; 5) ; Q(-2 ; 2 ; 3) ; R(-1 ; -2 ; 4) et S(5 ; 8 ; 4).

B. Les points P, Q et R sont alignés. Faux.
C. Le triangle PQR est isocèle en R. Vrai.
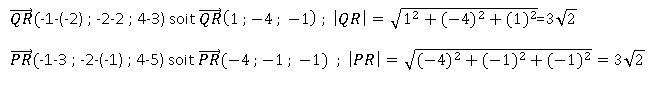
D. Les plans ( PQR) et (PQS) sont confondus. Vrai.
Hypothèse : les plans sont confondus.
Equation du plan ( PQR) : ax+by+cz=d.
P appartient à ce plan : 3a-b+5c= d ; (1)
Q appartient à ce plan : -2a+2b+3c=d ; (2) ; (1)-(2) donne : 5a -3b +2c=0.
R appartient à ce plan : -a-2b+4c=d ; (3)
S appartient à ce plan : 5a +8b+4c = d. (4) ; (4) -(3) donne : 6a+10b=0 ; b = -0,6 a.
5a +1,8a+2c = 0 ; 3,4a +c = 0 ; c = -3,4 a.
(2)+(3) donne : -3a+7c = 2d ; -3a-23,8 a = 2d ; d = -13,4 a.
(1) s'écrit : 3a +0,6a -17a =-13,4 a est vérifiée quel que soit a. l'hypothèse est vérifiée.

12. Soit
la fonction f définie par f(x) = x / 9 +1/6 sur [0 ; 3 ]. On note X la
variable aléatoire sur cet intervalle dont la loi de probabilité a pour
densité f.
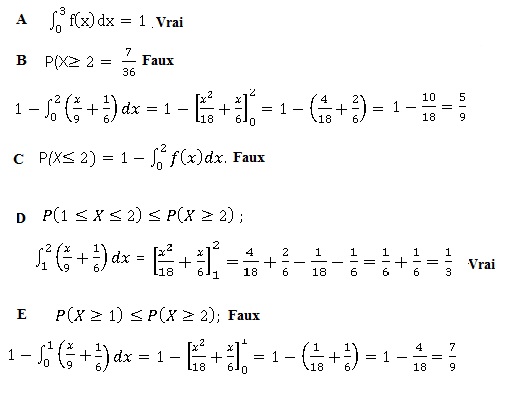
|
13. Dans
un restaurant sans réservation, on modélise le temps d’attente en
minutes pour obtenir une table par une variable aléatoire X. X suit une
loi exponentielle de paramètre l .
Une étude statistique a montré que le temps moyen d’attente est de 10 mn.
A. l = 10. Faux.
B. 1 / l = 10. Vrai.
C. La probabilité qu'un client attende entre 10 et 20 min est :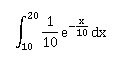 Vrai. Vrai.
D. La probabilité qu'un client attende plus de 20 min est 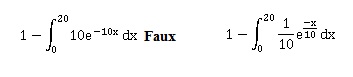
E. Un
client attend depuis 10 mn. La probabilité qu’il doive attendre encore
au moins 20 mn est égale à la probabilité qu’il attende plus de 20 mn.
Faux.
14.
On considère l’algorithme suivant dans lequel rand (1,7) donne un nombre entier aléatoire entre 1 et 7.
Variables i , j, k entiers naturels
Initialisation i=1, k =0
Traitement Tant que i < 6
j =rand (1,7)
Si j > 4 alors
k= k +1
Fin Si
i =i +1
Fin Tant que
Sortie Afficher k
(A) k est affiché lorsque j a été affecté 6 fois. Faux.
(B) La valeur affichée de k est une entier inférieur à 4. Vrai.
(C) La probabilité que k = 0 est égale à 4/7. Faux.
3 cas favorables sur 7 et la boucle " tant que" tourne 5 fois.
(D) La probabilité que k = 3 est égale à 4 (4/7)(3/7)4. Faux.
(E) La probabilité que k = 4 est égale à (3/7)5. Vrai.
3 cas favorables sur 7 et la boucle " tant que" tourne 5 fois.
|
|