Mathématiques,
Physique, Concours externe TSPEI 2017.
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1.
Soit la fonction f définie sur R par (x) = x e -x.
1. a Calculer f(0) etf(1). f(0) = 0 e -0 = 0 *1 = 0.
f(1) = 1 e -1 = 1 / e ~0,4.
1.b. Déterminer ces limites en plus l'infini et moins l'infini.
Quand x tend vers moins l'infini : x tend vers moins l'infini et e -x tend vers plus l'infini.
Par produit des limites, f(x) tend vers moins l'infini.
Quand x tend vers plus l'infini : x tend vers pluss l'infini et e-x = 1 /ex tend vers zéro.
Par produit des limites et croissance comparée x / ex, tend vers zéro.
2. Calculer la dérivée de f et donner le tableau de variations.
On pose u = x et v = e-x ; u' = 1 ; v' = -e-x ; u'v+v'u = e-x-xe-x = e-x(1-x).
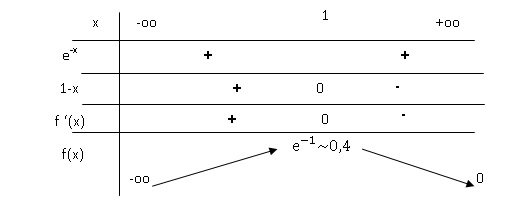 3.
3. Soit C la courbe représentative de f. Ecrire une équation de la tangente T à cette courbe en x = 0
Etudier la position de T par rapport à C. f '0) =1 ; équation de T : y = x+b.
La tangente passe à l'origine, donc b = 0.
Position de la courbe par rapport à T : xe -x-x = x(e -x-1).
Pour x >0, x(e-x-1) < 0, la tangente est au dessus de C.
Pour x < 0, x(e-x-1) < 0, la tangente est au dessus de C.
4. Construire C et T.
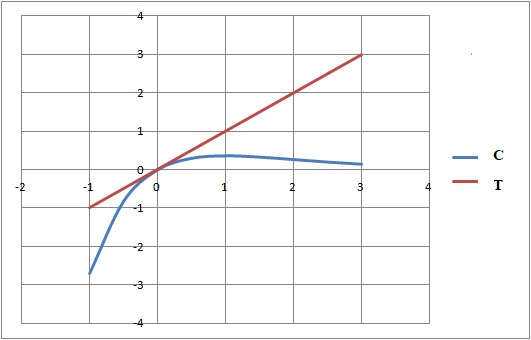
5.
Calculer en unité d'aire, l'aire du domaine compris entre la
tangente T, la courbe C et les droites d'équations x = 0 et x = 1.
Aire du triangle rectangle isocèle défini par T, l'axe des abscisses et la droite d'équation x=1 : 0,5
Aire du domaine compris entre la courbe C et les droites d'équation x=0 et x = 1 :
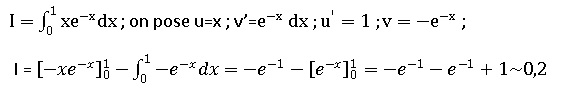
Aire recherchée : 0,5-(1-2 / e) ~0,3 unité d'aire.
|
| .
. |
....
...
|
Exercice 2.
1. Montrer que l'équation x4+1=0 n'admet pas de solution dans R.
On pose X = x2 ; X2+1=0 ;
Le déterminant étant négatif, X2+1 n'admet pas de solution dans R.
2. Résoudre dans C, l'équation z2+1=0.
z2 = -1 = i2 ; z = ± i.
3. En déduire dans C les solutions de l'équation z4+1=0.
Donner les solutions sous forme algébrique et sous forme trigonométrique.
On pose Z = z2 ; Z2+1 = 0 ; Z2 = -1 = i2.
Z = i = exp(ip / 2) ; z1 =exp(ip / 4)=cos 45 + i sin 45 = 0,707 +0,707 i.
z2 = - exp(ip / 4)= - cos 45 - i sin 45 = -0,707 -0,707 i.
Z = -i = exp(-ip / 2) ; z3 =exp(-ip / 4)=cos (-45) + i sin (-45) = 0,707 -0,707 i.
z4 = - exp(-ip / 4)= - cos (- 45) - i sin (-45) = -0,707 +0,707 i.
4. Déterminer les réels a, b, c et d tels que : x4+1 = (x2+ax+b)(x2+cx+d).
On développe : x4+1 =x4 +x3(c+a) +x2(d+ac+b)+x(ad+bc) +bd.
On identifie : bd = 1 ; a+c = 0 ; d+b+ac = 0 ; ad +bc = 0.
ad-ab = 0 ; b = d = 1 ; ac = -2 ; a2 = 2 ; a = 2½ ; c = -2½.
5. En déduire la décomposition en élément simples dans R de 1 / (x4+1).
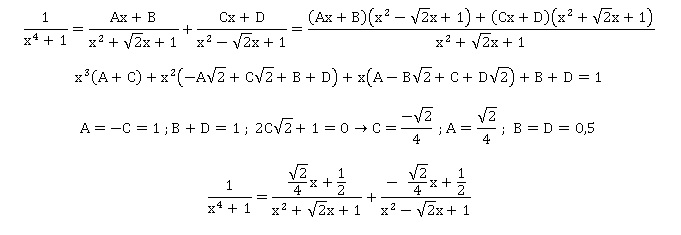
|
|
|
Exercice 3 .
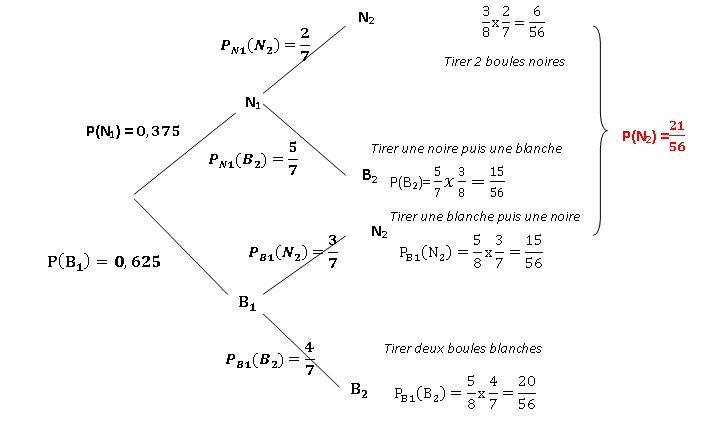
Une urne contient 8 boules : 3 noires et 5 blanches.
On tire une première boule sans la remettre dans l'urne et on note sa
couleur. On tire ensuite une seconde boule et on note sa couleur. On
supposera les tirages équiprobables. On note :
N1 : " on obtient une boule noire au premier tirage".
N2 : " on obtient une boule noire au second tirage".
B1 : " on obtient une boule blanche au premier tirage".
B2 : " on obtient une boule blanche au second tirage".
1. Déterminer la probabilité des événements N1 et B1.
P(N1) = 3 /8 = 0,375.
P(B1) =5 / 8 = 0,625.
2. On a obtenu une boule blanche au premier tirage. Quelle est la probabilité d'avoir une boule noire au second tirage ?
3 / 7
3. Quelle est la probabilité de tirer une boule blanche puis une boule noire ?
5 / 8 x 3 / 7 = 15 /56.
4. Calculer la probabilité de N2. Ce résultat était-il prévisible ?
On note X la variable aléatoire égale au nombre de boules blanches obtenues lors des deux tirages.
5.a. Donner dans un tableau la loi de X.
Nombre de boules blanches
|
0
|
1
|
2
|
Probabilité
|
6 / 56
|
30 / 56
|
20 / 56
|
5.b. Calculer l'espérance de X.
(0 x6 +1 x30 +2 x20) / 56=70 /56=35 /28 =5 / 4 = 1,25.
5.c. Interpréter le résultat précédent.
En recommençant un grand nombre de fois les tirages, on obtient en moyenne 1,25 boules blanches.
|
|
|
|
Déterlination d'un indice de réfraction.
1.1.a On considère un dioptre plan séparant l'air ( nair = 1,00) au dessus de l'eau ( neau
= 1,33). Un rayon lumineux arrive de bas en haut sur le dioptre avec
une incidence i. Faire un schéma en représentant les rayons incident,
réfracté et réfléchi. Donner la relation entre les angles r et i.
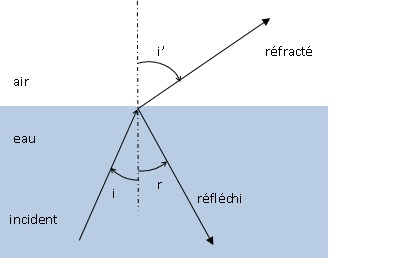 nair sin i' = neau sin i. nair sin i' = neau sin i.
1.1.b DLe
rayon réfracté existe-til toujours ? Déterminer l'angle d'incidence
limite au deà duquel le rayon est complétement réfléchi..
Le rayon réfracté n'existe pas toujours ( sin i' < 1 ).
A la limite de la réfraction ( réflexion totale) i' = 90 ° et sin i lim = nair / neau = 1 / 1,33 ~0,752; ilim ~48,6 °.
1.2.
On cherche à mesurer l'indice de réfraction n d'un liquide. On dispose
une goutte de liquide sur la face supérieure d'un prisme d'angle au
sommet 90 °. On éclaire cette goutte en lumière monochromatique sous
incidence rasante. A l'aide d'un oculaire, on observe derrière l'autre
face du prisme. l'indice du verre constituant le prisme est N = 1,625.
Schématiser la situation.
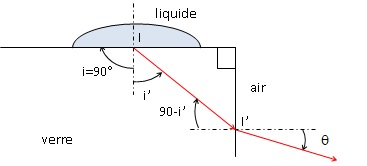
1.2.b. Exprimer q en fonction de n et N. Calculer n si q = 39°.
En I, il y a réflexion totale. sin i' = n / N soit i' = arcsin (n / N).
En I ' : N sin ( 90-i') = nair sin q.
N sin ( 90-arcsin (n / N)) = nair sin q.
q =arcsin[ N sin ( 90-arcsin (n / N))].
sin 39 / 1,625 =0,3873 = sin ( 90-i') ; 90-i' = 22,78 ; i' = 67,21°.
n = N sin i' = 1,625 sin 67,21 =1,498 ~1,5.
1.2.c Quelle est la valeur maximale nmax de l'indice de réfraction d'un liquide que l'on peut mesurer avec ce dispositif ?
nmax / N < 1 ; nmax = N = 1,625.
|
Panneaux photovoltaïques.
La caractéristique courant-tension d'une cellule photovoltaïque est donnée par : i = Is(1-exp(u /U0)) +a SE.
Is = 0,10 nA ; U0 = 25,8 10-3 V ; S = 12 cm2 ; a = 0,35 A W-1. S: surface de la cellule ; E : éclairement solaire.
1. Lorsque le flux solaire est maximal, E1= 800 W m-2. Par ciel voilé, l'éclairement vaut E2= 300 W m-2. Par temps gris, E3= 100 W m-2. Calculer la tension aux bornes de la cellule quand i = 0 pour les trois éclairements. On note Uc1, Uc2, Uc3 les tensions à vide aux bornes de la cellule, quand elle n'est pas branchée.
0= Is(1-exp(u /U0)) +a SE.
0 = 1,0 10-10(1-exp(u / 25,8) +0,35 x12 10-4 E.
1-exp(u / 25,8) = -0,35 x12 106 E.
exp(u / 25,8) =1+4,2 106 E.
u =25,8 ln(1+4,2 106 E) en mV.
U c1=25,8 ln (1+4,2 106 x800)~566 mV.
U c2=25,8 ln (1+4,2 106 x300)~541 mV.
U c3=25,8 ln (1+4,2 106 x100)~512 mV.
2. Calculer le courant de court-circuit ( lorsque la tension est nulle) pour les trois éclairement.
icc = Is(1-exp(0 /U0)) +a SE = a SE.
icc1 = 0,35 x12 10-4 x800 = 0,336 A.
icc2 = 0,35 x12 10-4 x300 = 0,126 A.
icc3 = 0,35 x12 10-4 x100 = 0,042 A.
Pour la suite, on envisage la cas où le flux solaire est maximum. La caractéristique de la cellule est :
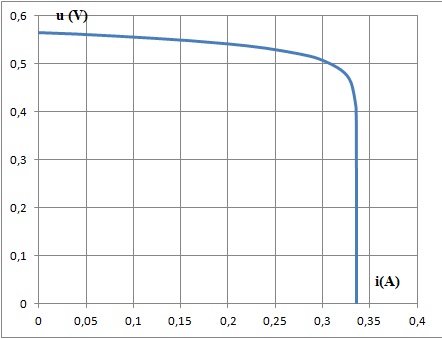
3. En quel point de la courbe la puissance est-elle maximale ? Que vaut Pmax.
Le produit u i doit être le plus grand possible.
Pmax = 0,156 W pour u = 0,32 V et i = 0,487 A.
4.
On définit le rendement de la cellule comme le rapport de la puissance
maximale sur la puissance solaire reçue. Calculer ce rendement.
Rendement = Pmax / (ES) = 0,156 /(800 x12 10-4) ~0,16 ( 16 %). Ce rendement est très faible.
5. On associe les cellules en série et en parallèle. On met en parallèle nP=25 branches identiques constituées de nS=50 cellules en série. Chaque cellule fournit sa puissance maximale.
Quelle est l'intensité du courant dans une branche ? Quelle est la
tension aux bornes de cette branche ? Quelle est l'intensité totale
délivrée par l'ensemble ?
Montrer que la puissance maximale est d'environ 200 W.
i= 0,487 A ; u = 50 x0,32 = 16 V. itotale = 0,487 x25~12,2 A.
Puissance = 16 x 12,2 ~195 W.
Pompe à chaleur.
Dans une pièce fermée on souhaite maintenir une température qamb = 20°C tandis que l'air extérieur est à qext = 0°C. On considère une pompe à chaleur.
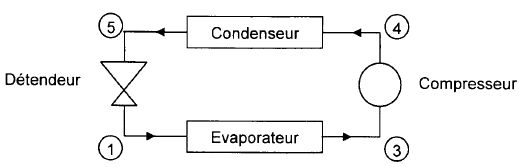
Le fluide est de l'hélium gazeux assimilé à un gaz parfait.
Cp = 5,26 kJ K-1 kg-1 ; M(He) = 4,0 g / mol ; g = 1,67.
Le fluide décrit des cycles :
- Détente adiabatique réversible dans le détendeur qui l'amène à l'état A ( qA = 20°C ; ; PA = 3,0 bar ) à l'état B ( TB ; PB = 2,0 bar).
- un réchauffement isobare dans l'échangeur qui amène le fluide à l'état C ( qC = 0°C ; PC).
- une compression adiabatique réversible dans le compresseur qui amène le fluide dans l'état D ( TD ; PD).
- un refroidissement isobare dans l'échangeur qui ramène le fluide dans l'état A.
1. Exprimer TB et TD en fonction de Tamb, Text, PA et PB. Faire les applications numériques.
On pose ß = (1-g) / g = -0,67 / 1,67 = -0,40.
Pour une transformation réversible adiabatique :
PAß TA = PBß TB ; TB =(PA / PB)ß Tamb =1,5-0,40 x 293 ~249 K.
PCß TC = PDß TD ; TD =(PC / PD)ß TC =(PB / PA)ß Text =(2 / 3)-0,40 x 273 ~321 K.
2. Donner l'allure du cycle en coordonnées (P, V) en précisant le sens de parcours.
3. Est-ce un cycle moteur ou récepteur ?
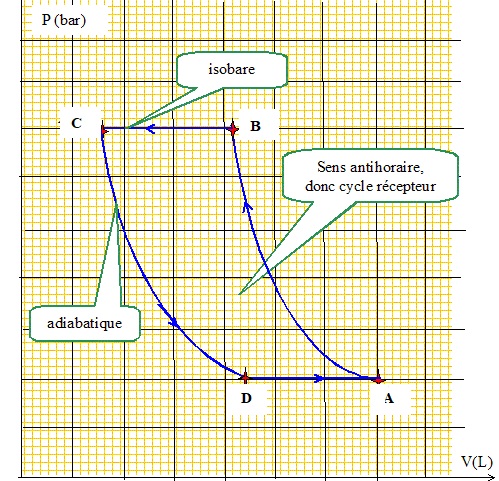
4. Calculer le tranfert thermique QBC reçu par une masse m = 1 kg de fluide lors de la traversée de l'échangeur EC ( extérieur). Commenter son signe.
Transformation isobare : QBC = m Cp (TC-TB) = 5,26 (273-249)=126,2 ~126 kJ.
Le fluide prèlève de la chaleur dans le milieu extérieur.
5. Calculer le tranfert thermique QDA reçu par une masse m = 1 kg de fluide lors de la traversée de l'échangeur EF( pièce ). Commenter son signe.
Transformation isobare : QDA = m Cp (TA-TD) = 5,26 (293-321)= -147,2 ~ -147 kJ.
Le fluide cède de la chaleur dans la pièce.
6. Calculer le travail reçu par 1 kg de fluide lors du cycle.
Premier principe de la thermodynamique, sur le cycle l'énergie interne de l'hélium ne varie pas.
W +QBC + QDA =0 ; W = - QBC - QDA = -126+147 ~21 kJ .
7. Définir l'efficacité de la pompe à chaleur et la calculer.
L'efficacité de la pompe, notée e,
est le rapport de la quantité de chaleur reçue par la source chaude au
cours d'un cycle décrit par le fluide, et du travail reçu par ce
fluide au
cours de ce même cycle.
e = |QDA| / W = 147 / 21 ~7.
8. Quel est l'intérêt de la pompe à chaleur par rapport à un chauffage électrique ?
Réduction de la facture énergétique : pour 1 kWh consommé, la PAC restitue 3 à 4 kWh de chaleur.
Chargement de minerai dans un wagon.
Un tapis roulant est utilisé pour charger du minerai dans un wagon. Longueur du tapis L = 20 m ; inclinaison avec l'horizontale a = 30° ; g = 10 m s-2.
1. Faire le bilan des forces s'exerçant sur un bloc de minerai de masse M = 20 kg entraîné à vitesse constante sur le tapis.
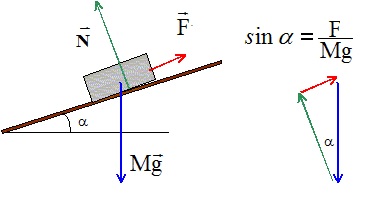
Poids, action normale du plan et frottements.
2. Calculer la valeur de la force de frottement exercée par le tapis roulant sur le bloc.
D'après la première loi de Newton, les forces se compensent.
F = Mg sin a = 20 x 10x sin 30 = 100 N.
3. Calculer le travail de cette force lorsque le bloc parcourt la longueur L.
W = F L = 100 x 20 = 2000 J = 2 kJ.
4. Quelle est la
puissance des forces exercées par le tapis sur le minerai transporté si
la vitesse de chargement du wagon est 1,55 tonne par minute ?
L'action normale du plan étant perpendiculaire à la vitesse du tapis, son travail, donc sa puissance sont nulles.
1,55 x1000 / 60 = 25,83 kg s-1.
Durée de chargement de 20 kg = durée du parcours L =20 / 25,83 ~ 0,774 s.
Puissance de F : 2 / 0,774 ~2,6 kW.
|
|


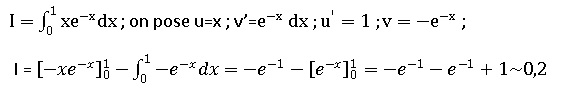
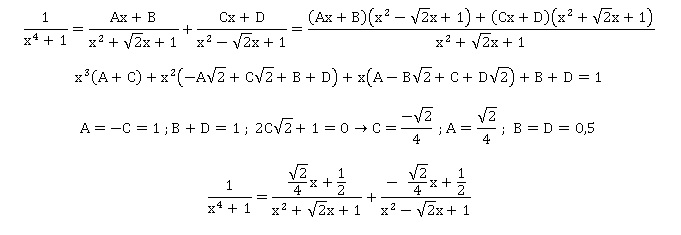

 nair sin i' = neau sin i.
nair sin i' = neau sin i.



